��Ŀ����
����Ŀ�������������٣�ij��ҵ����������Ͷ�빲�����������г��������絥�����綯������2000������֪ÿ�����������ɱ�380Ԫ��ÿ̨�����絥���ɱ�1500Ԫ��2������������1�������絥��ÿ��ë��31Ԫ��4������������3�������絥��ÿ��ë��81Ԫ��
��1���������������絥��ÿ��ÿ���ֱ����ӯ������Ԫ��
��2��Ϊ����Ͷ�ʻر��ʣ�����ҵ�ƻ�Ͷ��ɱ�������174��Ԫ��ÿ�ܵ�ë��������23050Ԫ����Ҫ��Ͷ��ĵ�������Ϊ10�ı����������оٳ�����Ͷ���ʽ���
���𰸡���1���������������絥��ÿ��ÿ���ֱ����ӯ��6Ԫ��19Ԫ����2��������.
��������
��1�����蹲�����������綯��ÿ��ÿ���ֱ����ӯ��xԪ��yԪ�����������г���������⼴�ɣ�
��2����Ͷ��Ĺ�����������Ϊ10n�������������г�����n�IJ���ʽ�飬�������ʽ��Ľ⼯���ٽ��nΪ��Ȼ��ȷ��n�ľ���ֵ�����д����������.
�⣺�蹲������ÿ��ÿ������ӯ��xԪ�������絥��ÿ��ÿ������ӯ��yԪ��
�������⣬��![]()
���![]()
�𣺹������������絥��ÿ��ÿ���ֱ����ӯ��6Ԫ��19Ԫ.
��2����Ͷ��Ĺ�����������Ϊ10n����
��Ͷ��Ĺ����絥������Ϊ��2000��10n����.
���������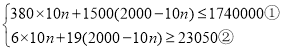
�ⲻ��ʽ�ٵã�![]() ��
��
�ⲻ��ʽ�ڵã�![]() ��
��
��ԭ����ʽ��Ľ⼯Ϊ![]() .
.
������֪nΪ��Ȼ����
��n��ȡ��ֵΪ113,114,115.
��n=113ʱ��10��113=1130��������2000��1130=870��������
��n=114ʱ��10��114=1140��������2000��1140=860��������
��n=115ʱ��10��115=1150��������2000��1150=850������.
��Ͷ���ʽ�Ϊ��
����һ��Ͷ�빲������1130���������絥��870����
��������Ͷ�빲������1140���������絥��860����
��������Ͷ�빲������1150���������絥��850��.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������50����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±��������е�һ��ͳ�����ݣ�
������Ĵ��� | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ��� | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
��������ĸ��� | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������Ƶ�![]() �ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
�ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
��2�����������һ�Σ���������ĸ���P��������______��
��3���Թ���������ɫ�����ж��ٸ���