题目内容
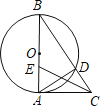
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
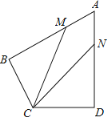
【答案】120 ;![]()
【解析】
试题分析:∵在四边形ABCD中, AB⊥BC,AD⊥CD,∠BAD=60°, ∴∠BCD=360°-90°-90°-60°=120°;
连接MN,连接AC,
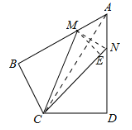
∵AB=AD=6,AM:MB=AN:ND=1:2,∴AM=AN=2,BM=DN=4,∵∠MAN=60°,∴△MAN是等边三角形,∴MN=AM=AN=2,
∵在Rt△ABC与Rt△ADC中,![]() ,∴Rt△ABC≌Rt△ADC(HL),∴∠BAC=∠DAC=
,∴Rt△ABC≌Rt△ADC(HL),∴∠BAC=∠DAC=![]() ∠BAD=30°,MC=NC,∴BC=
∠BAD=30°,MC=NC,∴BC=![]() AC,∴AC2=BC2+AB2,即(2BC)2=BC2+AB2,3BC2=AB2,∴BC=
AC,∴AC2=BC2+AB2,即(2BC)2=BC2+AB2,3BC2=AB2,∴BC=![]() ,
,
在Rt△BMC中,CM=![]() =
=![]()
![]() ,
,
过M点作ME⊥ON于E,设NE=x,则CE=![]() -x,
-x,
∴MN2-NE2=MC2-EC2,即4-x2=(![]() )2-(
)2-(![]() -x)2,
-x)2,
解得:x=![]() ,∴EC=
,∴EC=![]() -
-![]() =
=![]() ,∴cos∠MCN=
,∴cos∠MCN=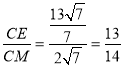 .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变