题目内容
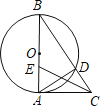
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,∠DAC=∠B.
(1)求证:CA是⊙O的切线.
(2)在AB上取一点E,若∠BCE=∠B,AB=2AC,求tan∠ACE的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据圆周角定理可知∠ADB=90°,再根据∠DAC=∠B和等量代换可知∠BAC=90°,从而可证CA是⊙O的切线;
(2)将⊙O的半径为r,EC=x,在Rt△AEC中,通过勾股定理找到x与r之间的关系,从而表示出AE,AC,利用![]() 即可求解.
即可求解.
(1)证明:∵AB是直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵∠DAC=∠B,
∴∠DAC+∠BAD=90°,
∴∠BAC=90°,
∴BA⊥AC,
∴AC是⊙O的切线.
(2)解:设⊙O的半径为r,EC=x,
∵AB=2AC,
∴AC=r,
∵∠BCE=∠B,
∴EB=EC=x,
∴AE=2r﹣x
在Rt△AEC中,EC2=AE2+AC2,
即x2=(2r﹣x)2+r2,
解得![]()
![]()
![]()

练习册系列答案
相关题目