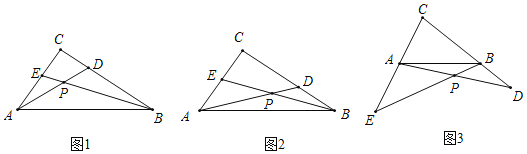
题目内容
【题目】已知:△ABC是等腰三角形,CA=CB,0°<∠ACB≤90°.点M在边AC上,点N在边BC上(点M、点N不与所在线段端点重合),BN=AM,连接AN,BM,射线AG∥BC,延长BM交射线AG于点D,点E在直线AN上,且AE=DE.
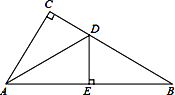
(1)如图,当∠ACB=90°时
①求证:△BCM≌△ACN;
②求∠BDE的度数;
(2)当∠ACB=α,其它多件不变时,∠BDE的度数是 (用含α的代数式表示)
(3)若△ABC是等边三角形,AB=3![]() ,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
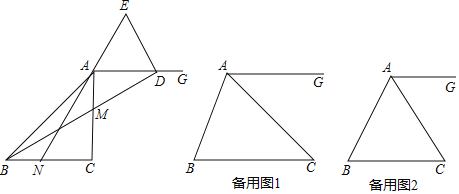
【答案】(1)①证明见解析;②∠BDE=90°;(2)α或180°﹣α;(3)CF的长为![]() 或4
或4![]() .
.
【解析】(1)①根据SAS证明即可;
②想办法证明∠ADE+∠ADB=90°即可;
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上时,②如图3中,当点E在NA的延长线上时,
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,解直角三角形即可.②如图5中,当CN=
时,作AK⊥BC于K,解直角三角形即可.②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,结合图形求解即可.
时,作AK⊥BC于K,DH⊥BC于H,结合图形求解即可.
(1)①如图1中,
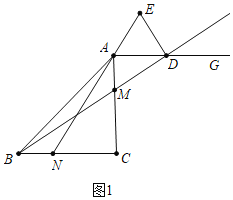
∵CA=CB,BN=AM,
∴CB﹣BN=CA﹣AM,
即CN=CM,
∵∠ACN=∠BCM,
∴△BCM≌△CAN;
②如图1中,
∵△BCM≌△ACN,
∴∠MBC=∠NAC,
∵EA=ED,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠GAC=∠ACB=90°,∠ADB=∠DBC,
∴∠ADB=∠NAC,
∴∠ADB+∠EDA=∠NAC+∠EAD,
∵∠ADB+∠EDA=180°﹣90°=90°,
∴∠BDE=90°;
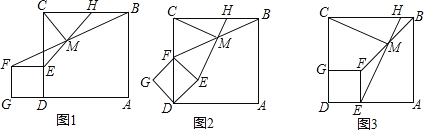
(2)如图2中,当点E在AN的延长线上时,
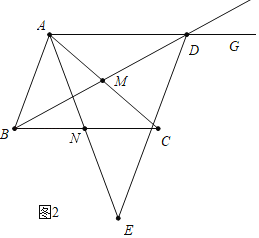
易证:∠CBM=∠ADB=∠CAN,∠ACB=∠CAD,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠CAN+∠CAD=∠BDE+∠ADB,
∴∠BDE=∠ACB=α;
如图3中,当点E在NA的延长线上时,
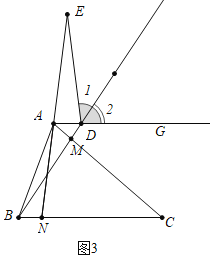
易证:∠1+∠2=∠CAN+∠DAC,
∵∠2=∠ADM=∠CBD=∠CAN,
∴∠1=∠CAD=∠ACB=α,
∴∠BDE=180°﹣α,
综上所述,∠BDE=α或180°﹣α,
故答案为:α或180°﹣α;
(3)如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,
时,作AK⊥BC于K,
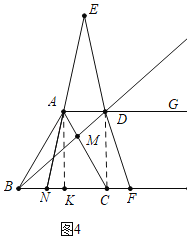
∵AD∥BC,
∴![]() ,
,
∴AD=![]() ,AC=3
,AC=3![]() ,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,
,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,
∴CF=NK=BK﹣BN=![]() ﹣
﹣![]() =
=![]() ;
;
如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,
时,作AK⊥BC于K,DH⊥BC于H,
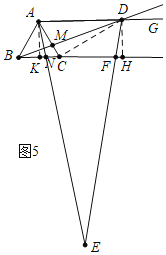
∵AD∥BC,
∴![]() ,
,
∴AD=6![]() ,易证△ACD是直角三角形,
,易证△ACD是直角三角形,
由△ACK∽△CDH,可得CH=![]() AK=
AK=![]() ,
,
由△AKN≌△DHF,可得KN=FH=![]() ,
,
∴CF=CH﹣FH=4![]() .
.
综上所述,CF的长为![]() 或4
或4![]() .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案