题目内容
【题目】 完成下面的证明.
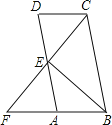
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
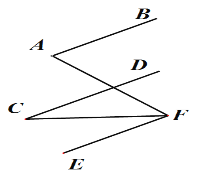
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
【答案】∠A—∠C; ∠AFE, 两直线平行,内错角相等; ∠CFE, 两直线平行,内错角相等; ∠AFE, ∠CFE;∠A—∠C ,等量代换.
【解析】
根据平行线的性质得∠A=∠AFE,∠C=∠CFE,在利用角的和差即可得出答案.
解:∠AFC= ∠A—∠C 理由如下:
∵AB∥EF(已知),
∴∠A= ∠AFE (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ∠CFE ( 两直线平行,内错角相等).
∵∠AFC= ∠AFE - ∠CFE
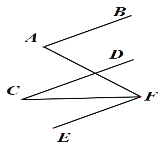
∴∠AFC= ∠A—∠C (等量代换).

练习册系列答案
相关题目
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
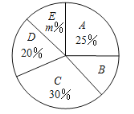
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.