题目内容
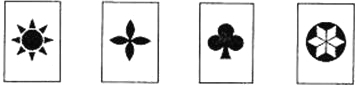
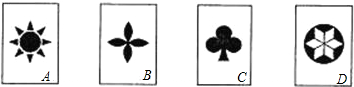
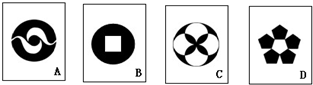
有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后任意摸出两张.
(1)用树状图(或列表法)表示所摸的两张牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌的牌面图形能组合成轴对称图形的纸牌的概率.
分析:列举出所有情况,看摸出两张牌的牌面图形能组合成轴对称图形的情况数占所有情况数的多少即可.
解答:解:(1)
(2)一共有12种结果,每种结果出现的可能性相同,能组合成轴对称图形的情况数有6种,
∴P(两张牌的牌面图形能组合成轴对称的纸牌)=
;
答:摸出两张牌的牌面图形能组合成轴对称图形的纸牌的概率是
.
| 第一次 第二次 |
A | B | C | D |
| A | (B,A) | (C,A) | (D,A) | |
| B | (A,B) | (C,B) | (D,B) | |
| C | (A,C) | (B,C) | (D,C) | |
| D | (A,D) | (B,D) | (C,D) |
∴P(两张牌的牌面图形能组合成轴对称的纸牌)=
| 1 |
| 2 |
答:摸出两张牌的牌面图形能组合成轴对称图形的纸牌的概率是
| 1 |
| 2 |
点评:考查概率问题;得到摸出两张牌的牌面图形能组合成轴对称图形的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
相关题目