Question

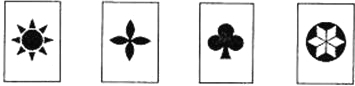
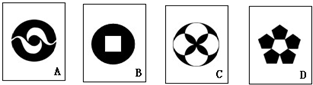
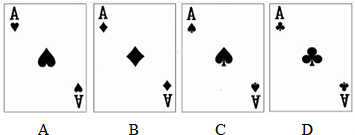
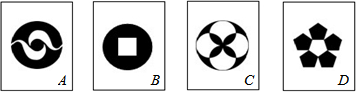
如图，有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的图形，小明将这四张纸牌背面朝上洗匀后随机摸出一张，再随机摸出一张（不放回）．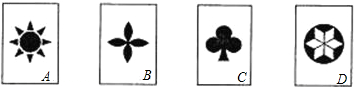

（1）随机摸一张牌是轴对称图形的概率是多少？
（2）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A，B，C，D表示）；
（3）求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率．

Answer 1

分析：（1）纸牌A、B、C、D都是轴对称图形，故其概率是1．
（2）画出树状图分析数据、列出可能的情况．
（3）A、B、D既是轴对称图形，也是中心对称图形，C是轴对称图形，不是中心对称图形．列举出所有情况，让两次摸牌的牌面图形既是中心对称图形又是轴对称图形的情况数除以总情况数即为所求的概率．

解答：解：（1）纸牌A、B、C、D都是轴对称图形，随机摸一张牌是轴对称图形的概率是1．

（2）画树状图如下所示：

所以可能出现的结果有12种：（A，B），（A，C），（A，D），（B，A），（B，C），（B，D），（C，A），（C，B），（C，D），（D，A），（D，B），（D，C）．

（3）由（2）可知，两次摸牌所有可能出现的结果共有12种，其中既是中心对称图形又是轴对称图形的有6种，故所求概率是

1

2

．

点评：本题考查了列表法与树状图法的知识，用到的知识点为：概率=所求情况数与总情况数之比．