Question

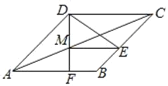
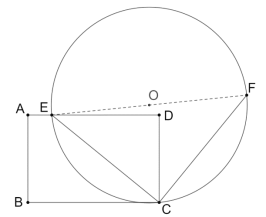
【题目】如图，点在矩形的边上，，，连接，线段绕点旋转，得到线段，以线段为直径做．

（1）请说明点一定在上的理由，

（2）①点在上，为的直径，求证：点到的距离等于线段的长．

②当面积取得最大值时，求半径的长．

（3）当与矩形的边相切时，计算扇形的面积．

Answer 1

【答案】（1）证明见解析；（2）①证明见解析，②；（3）

【解析】

（1）由CE=CF且∠ECF=90°，O为EF中点，可知OC=OE=OF=，即E，F，C三点共圆；

（2）①作MN⊥AD交AD于点N，连MC，MF，AC，由为的直径，且四边形ABCD为矩形可证得∠DCE=∠MEN，由CM为直径，可得，由（1）知∠FEC=45°，则可得∠MEO=45°，则易知∠EMO=45°，可得MC⊥EF，可证得四边形ECFN为正方形，所以EC=EM，可证△MEN≌△ECD，即MN=ED，证得M到AD的距离等于ED的长；

②设AE=x，则，，，即当x=3时，△AME面积有最大值为，由可知，即，而，由，求得，即的半径为；

（3）与矩形的边相切时，点O与点D重合，CO=MO为直径，且长为4，则可求得．

解：（1）依题意可知，CE=CF且∠ECF=90°，O为EF中点，

∴OC=OE=OF=，

∴点E，F，C三点在上；

（2）①作MN⊥AD交AD于点N，连MC，MF，AC，

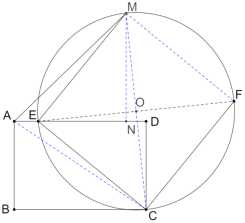
∵为的直径，

∴∠DEC+∠DEM=90°，

∵四边形ABCD为矩形，

∴∠DEC+∠DCE=90°

∴∠DCE=∠MEN，

∵CM为直径，

∴，

由（1）知∠FEC=45°，

∴∠MEO=45°，

∵OM=OE，

∴∠EMO=45°，

∴MC⊥EF，

∴四边形ECFN为正方形，

∴EC=EM，

在△MEN和△ECD中，

，

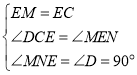所以△MEN≌△ECD，

∴MN=ED，

∴M到AD的距离等于ED的长；

②设AE=x，

∴，

∴，

∴，

∴，

∴当x=3时，△AME面积有最大值为，

∵，

∴，

∴，

又∵，

∴，

又∵，

∴，

即的半径为；

（3）与矩形的边相切时，点O与点D重合CO，MO为直径，长为4，

∴．