题目内容
【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
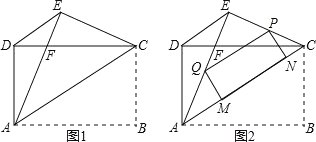
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
【答案】(1)证明见解析;(2)DF=![]() .(3) PE=
.(3) PE=![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.
【解析】试题分析:(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以![]() ,从而求得PQ,由PN∥EG,得出
,从而求得PQ,由PN∥EG,得出![]() ,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
试题解析:(1)由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,
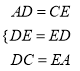
∴△DEC≌△EDA(SSS);
(2)如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=![]() ,
,
即DF=![]() .
.
(3)如图2,
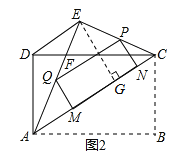
由矩形PQMN的性质得PQ∥CA
∴![]()
又∵CE=3,AC=![]() =5
=5
设PE=x(0<x<3),则![]() ,即PQ=
,即PQ=![]() x
x
过E作EG⊥AC于G,则PN∥EG,
∴![]()
又∵在Rt△AEC中,EGAC=AECE,解得EG=![]() ,
,
∴![]() =
=![]() ,即PN=
,即PN=![]() (3-x),
(3-x),
设矩形PQMN的面积为S,
则S=PQPN=-![]() x2+4x=-
x2+4x=-![]() (x-
(x-![]() )2+3(0<x<3)
)2+3(0<x<3)
所以当x=![]() ,即PE=
,即PE=![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?