题目内容
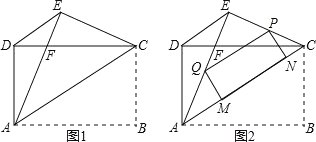
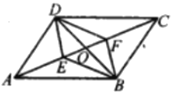
【题目】如图,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,解答下列问题:
,解答下列问题:
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.
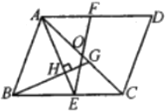
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)证明![]() ≌
≌![]() 可得
可得![]() ,再结合平行四边形对边相等即可得到结论;
,再结合平行四边形对边相等即可得到结论;
(2)①过A作AM⊥BC于M,交BG于K,根据三角形的外角性质得到∠BAG=∠BGA,由此可得AB=BG;②过G作GN⊥BC于N,证明![]() ≌
≌![]() ,可求得BM,再根据等腰三角形三线合一即可求得BE,从而求得DF.
,可求得BM,再根据等腰三角形三线合一即可求得BE,从而求得DF.
(1)∵四边形![]() 是平行四边形,
是平行四边形,
∴AD∥BC,AD=BC,
![]() ,
,
∵点![]() 是对角线
是对角线![]() 的中点,
的中点,
∴AO=CO,
在![]() 和
和![]() 中,
中,
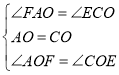 ,
,
∴![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
(2)①过A作AM⊥BC于M,交BG于K,
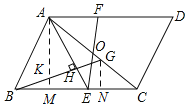
则∠AMB=∠AME,
∵∠ACB=45°,
∴∠MAC=45°,
∵AB=AE,![]() ,
,
∵AE⊥BG,
∴∠AHK=90°=∠BMK,又∠AKH=∠BKM,
∴∠MAE=∠CBG,
设∠BAM=∠MAE=∠CBG=α,则∠BAG=45°+α,∠BGA=∠GCB+∠GBC=45°+α,
∴∠BAG=∠BGA,
∴AB=BG;
②过G作GN⊥BC于N,
∴∠BNG=∠GNC=90°,
∵∠ACB=45°,
∴∠NGC =45°,
∴NG=NC,
在![]() 和
和![]() 中,
中,
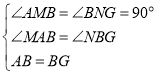 ,
,
∴![]() ≌
≌![]() ,
,
![]() ,
,
在Rt△NGC中,
根据勾股定理![]() ,
,
![]() ,
,
![]() .
.

【题目】南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h) | 路程(km) | 时间(h) | |
大巴车 | x | 120 | ________ |
小汽车 | ________ | 120 | ________ |
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?