题目内容
【题目】如图,![]() ,
,![]() ,
,![]() .动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为
.动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为![]() ,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.
,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.

(1)当![]() 时,求l的解析式;
时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)求出t为何值时,点M关于l的对称点落在坐标轴上.
【答案】(1) ![]() ;(2) 6<t<9;(3) 2秒或3秒.
;(2) 6<t<9;(3) 2秒或3秒.
【解析】
(1)将P(0,4)代入解析式中即可求解;
(2)当直线l刚好经过M点时求出其与y轴的交点坐标,进而求出P点运动的路程,再除以速度进而得到时间;当直线l刚好经过N点时同样的方式求出时间,两个时间之间即为t的取值范围;
(3)作M点关于l的对称点M’,求出M’坐标,再分别令其横坐标和纵坐标为0,求出t的值.
解:(1)当![]() 时,此时P点的坐标为(0,5),将(0,5)代入解析式
时,此时P点的坐标为(0,5),将(0,5)代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]()
故![]() 时,求l的解析式为:
时,求l的解析式为:![]() .
.
故答案为:![]() .
.
(2)当直线l经过点![]() 时,将点
时,将点![]() 代入解析式
代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]() ,此时l的解析式为:
,此时l的解析式为:![]()
令![]() ,∴此时P点的坐标为
,∴此时P点的坐标为![]()
又∵运动的速度为1个单位每秒,故此时运动了7-1=6秒;
当直线l经过点![]() 时,将点
时,将点![]() 代入解析式
代入解析式![]() 中
中
得到:![]() ,解得:
,解得:![]() ,此时l的解析式为:
,此时l的解析式为:![]()
令![]() ,∴此时P点的坐标为
,∴此时P点的坐标为![]()
又∵运动的速度为1个单位每秒,故此时运动了10-1=9秒;
故当6<t<9时点M,N位于l的异侧.
故答案为:6<t<9.
(3) 作M点关于l的对称点M’,如下图所示:
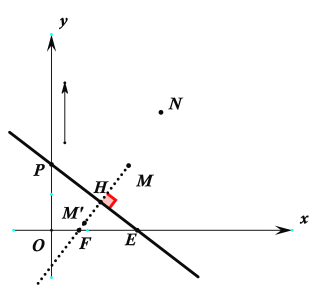
连接MM’与x轴交于点F,直线l与x轴交于E点,直线l与MM’交于点H
则有MM’⊥HE,∴∠EHF=90°
∵直线l与x轴所夹的锐角为45°
∴∠MFE=90°-45°=45°
∴直线MM’解析式中的k=1,设MM’解析式为y=x+n,
代入点M(4,3),解得n=-1
故直线MM’的解析式为:y=x-1
∴设点M’的坐标为(![]() ),
),
由H是M和M’的中点可知:
H点坐标为![]() ,即H
,即H![]()
情况一:当M’位于x轴上时,即![]() ,即
,即![]() 时,
时,
求得H点坐标为(![]()
又H点在直线l上,故将H点坐标代入直线l的解析式![]() 中
中
求得![]() ,此时l的解析式
,此时l的解析式![]()
∴此时P点坐标为(0,4)
故时间t=(4-1)÷1=3秒;
情况二:当M’位于y轴上时,即![]() 时
时
求得H点坐标为(![]()
又H点在直线l上,故将H点坐标代入直线l的解析式![]() 中
中
求得![]() ,此时l的解析式
,此时l的解析式![]()
∴此时P点坐标为(0,3)
故时间t=(3-1)÷1=2秒;
故答案为:2秒或3秒.

 名校课堂系列答案
名校课堂系列答案【题目】南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h) | 路程(km) | 时间(h) | |
大巴车 | x | 120 | ________ |
小汽车 | ________ | 120 | ________ |
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.