Question

已知点A（a，0）、B（b，0），且．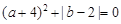

（1）求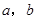的值；
（2）在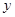轴上是否存在点C，使得△ABC的面积是12？若存在，求出点C的坐标；若不存在，请说明理由；
（3）点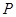是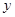轴正半轴上一点，且到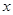轴的距离为3，若点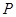沿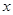轴负半轴方向以每秒1个长度单位平行移动至Q，当运动的时间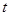为多少秒时，四边形ABPQ的面积S为15个平方单位？写出此时Q点的坐标．

Answer 1

（1）a=-4，b=2；（2）（0，4），（0，-4）；（3）

解析试题分析：（1）根据题中等式（a+4）的平方和（b-2）的绝对值都为非负数可直接求出a，b的值；
（2）根据三角形面积的定义，可知只要OC长为4，三角形面积AC×OA就等于12，所以存在两个C点满足题意；
（3）先得到点P的坐标，设，根据梯形的面积公式可得，从而可以求得结果.
（1）．
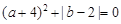a=-4，b=2
（2）根据三角形面积定义我们可知，只要OC长为4就满足题意，
∴在A点上下分别有一个C满足题意，坐标分别为（0，4），（0，-4）．
（3）由题意得P(0，3)
设，则



考点：坐标与图形的性质
点评：本题知识点较多，综合性强，难度较大，是中考常见题，要特别注意.