题目内容
【题目】如图,直线y=-2x+2与抛物线y=ax2+bx(a<0)相交于点A,B.双曲线y=![]() 过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=
过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=![]() .
.
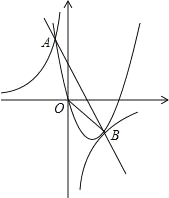
(1)求双曲线和抛物线的解析式;
(2)计算△AOB的面积;
(3)在抛物线上是否存在点P,使△AOP的面积等于△AOB的面积?若存在,请你写出点P的坐标;若不存在,请你说明理由.
【答案】(1)双曲线解析式为y=-![]() ,抛物线解析式为y=x2-3x,(2)3,(3)P(-3,18).
,抛物线解析式为y=x2-3x,(2)3,(3)P(-3,18).
【解析】
试题分析:(1)先用待定系数法求出双曲线解析式,再用待定系数法求出抛物线解析式;
(2)先求出△AOB的面积,在求出△BOC的面积即可;
(3)先求出直线PB解析式为y=-4x+6,和抛物线解析式为y=x2-3x,联立方程组求解即可.
试题解析:(1)∵双曲线经过点B,
∴k=-4,
∴双曲线解析式为y=-![]() ,
,
∵tan∠AOy=![]() ,
,
设A(-m,4m),
∵点A 过双曲线,
∴m=1或m=-1(舍),
∴A(-1,4);
∵抛物线过点A,B,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2-3x,
(2)设直线y=-2x+2交于x轴于C,令y=0,
∴x=1,
∴OC=1,
∴S△AOB=S△AOC+S△BOC=![]() ×1×4+
×1×4+![]() ×1×2=3,
×1×2=3,
(3)存在点P(-3,18),
理由:假设存在点P,使△AOP的面积等于△AOB的面积;
∴点P到直线OA的距离等于点B到直线OA的距离,
∴PB∥AO,
∵直线AO解析式为y=-4x,
∴设直线PB的解析式为y=-4x+f,
∵直线PB过点B,
∴-2=-4×2+f,
∴f=6,
∴直线PB解析式为y=-4x+6,
∴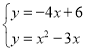 ,
,
∴![]() 或
或![]() (舍),
(舍),
P(-3,18).

练习册系列答案
相关题目
