题目内容
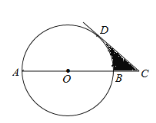
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D.若∠C =45°,AB=8.
(1)求BC的长;
(2)求阴影部分的面积(结果保留π).
【答案】(1)BC=![]() ;(2)
;(2)![]()
【解析】
(1)连接OD,由CD为圆O的切线,根据切线的性质得到OD与CD垂直,可得三角形OCD为直角三角形,同时由直径AB的长求出半径OC的长,根据锐角三角函数定义得到sinC为∠C的对边OD与斜边OC的比值,即可求出OC的长,则BC=OC-OB,可得出BC的长;
(2)由直角三角形中∠C的度数,根据直角三角形的两个锐角互余求出∠DOC的度数,求得CD的长度,利用直角三角形两直角边乘积的一半求出直角三角形COD的面积,利用扇形的面积公式求出扇形BOD的面积,用三角形COD的面积减去扇形COE的面积,即可求出阴影部分的面积.
(1)连接OD,
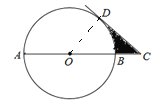
∵CD切⊙O于点D,
∴OD⊥CD,
∵AB=8,
∴OB=OD=![]() AB=4,
AB=4,
又在直角三角形OCD中,∠C=45°,
∴sinC=sin45°=![]() ,
,
即OC=![]() ,
,
∴BC=OC-OB=![]() ;
;
(2)∵∠OCD=90°,∠C=45°,
∴∠COD=45°,
∴CD=OD=4,
∴S△COD=![]() CD·OD=
CD·OD=![]() =8,
=8,
∴S扇形BOD=![]() =2π,
=2π,
则S阴影= S△COD - S扇形BOD =8-2π.

练习册系列答案
相关题目