题目内容
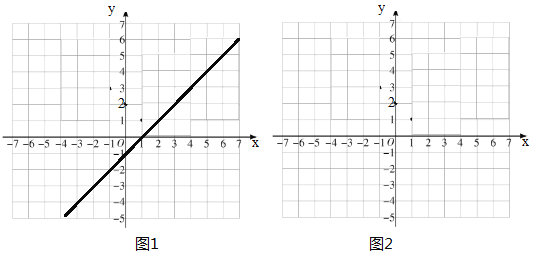
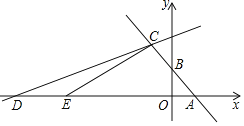
【题目】如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=![]() x+b的图象交于点C(﹣2,m).
x+b的图象交于点C(﹣2,m).
(1)求m和b的值;
(2)函数y=![]() x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
【答案】(1)m的值是4,b的值是![]() ;(2)①当△ACE的面积为12时,t的值是5;②存在,当t=4或t=6时,△ACE是直角三角形.
;(2)①当△ACE的面积为12时,t的值是5;②存在,当t=4或t=6时,△ACE是直角三角形.
【解析】
(1)将点C坐标代入直线y=﹣x+2中即可求出m的值,从而求出点C的坐标,然后将点C的坐标代入y=![]() x+b中即可求出b的值;
x+b中即可求出b的值;
(2)①根据两个一次函数的解析式分别求出点A、B、D的坐标,从而求出AD,由题意可得,DE=2t,则AE=16﹣2t,然后利用三角形的面积公式列出方程即可求出t的值;
②根据直角三角形直角顶点的情况分类讨论:当∠ACE=90°时,AC⊥CE,根据平面直角坐标系中任意两点之间的距离公式即可求出AC,证出△ACE为等腰直角三角形即可求出AE然后列方程即可求出t;当∠CEA=90°时,证出△ACE为等腰直角三角形即可求出AE然后列方程即可求出t.
(1)∵点C(﹣2,m)在直线y=﹣x+2上,
∴m=﹣(﹣2)+2=2+2=4,
∴点C(﹣2,4),
∵函数y=![]() x+b的图象过点C(﹣2,4),
x+b的图象过点C(﹣2,4),
∴4=![]() ×(﹣2)+b,得b=
×(﹣2)+b,得b=![]() ,
,
即m的值是4,b的值是![]() ;
;
(2)①∵函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,
∴点A(2,0),点B(0,2),
∵函数y=![]() x+
x+![]() 的图象与x轴交于点D,
的图象与x轴交于点D,
∴点D的坐标为(﹣14,0),
∴AD=16,
由题意可得,DE=2t,则AE=16﹣2t,
∵△ACE的面积为12,点C的坐标为(﹣2,4),
∴![]() =12,
=12,
解得,t=5
即当△ACE的面积为12时,t的值是5;
②当t=4或t=6时,△ACE是直角三角形,
理由:当∠ACE=90°时,AC⊥CE,
∵点A(2,0),点B(0,2),点C(﹣2,4),点D(﹣14,0),
∴OA=OB,AC=![]() 4
4![]() ,
,
∴∠BAO=45°,
∴∠CAE=45°,
∴∠CEA=45°,
∴CA=CE=4![]() ,
,
∴△ACE为等腰直角三角形
∴AE=8,
∵AE=16﹣2t,
∴8=16﹣2t,
解得,t=4;
当∠CEA=90°时,
∵AC=4![]() ,∠CAE=45°,
,∠CAE=45°,
∴△ACE为等腰直角三角形
∴AE=4,
∵AE=16﹣2t,
∴4=16﹣2t,
解得,t=6;
由上可得,当t=4或t=6时,△ACE是直角三角形.


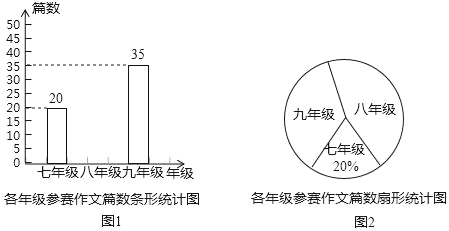
【题目】某学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制作了不完整的统计图表.
学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 6 | 15 | a | 12 | 9 |
学生借阅图书的次数扇形统计图

请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该样本数据的中位数是 次,众数是 次;
(3)请计算扇形统计图中“3次”所对应的扇形圆心角的度数;
(4)若该校共有2400名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.