题目内容
【题目】已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点. 
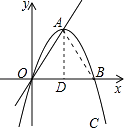
(1)如图1,若∠AOB=60°,求抛物线C的解析式;
(2)如图2,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线C′,求抛物线C、C′的解析式;
(3)在(2)的条件下,设A′为抛物线C′的顶点,求抛物线C或C′上使得PB=PA′的点P的坐标.
【答案】
(1)解:连接AB.
∵A点是抛物线C的顶点,且抛物线C交x轴于O、B,
∴AO=AB,
又∵∠AOB=60°,
∴△ABO是等边三角形,
过A作AD⊥x轴于D,在Rt△OAD中,
∴OD=2,AD= ![]() ,
,
∴顶点A的坐标为(2, ![]() )
)
设抛物线C的解析式为 ![]() (a≠0),
(a≠0),
将O(0,0)的坐标代入,
求得:a=- ![]() ,
,
∴抛物线C的解析式为 ![]()
(2)解:过A作AE⊥OB于E,
∵抛物线C:y=ax2+bx+c(a<0)过原点和B(4,0),顶点为A,
∴OE= ![]() OB=2,
OB=2,
又∵直线OA的解析式为y=x,
∴AE=OE=2,
∴点A的坐标为(2,2),
将A、B、O的坐标代入y=ax2+bx+c(a<0)中,
∴a=- ![]() ,
,
∴抛物线C的解析式为 ![]() ,
,
又∵抛物线C、C′关于原点对称,
∴抛物线C′的解析式为 ![]()
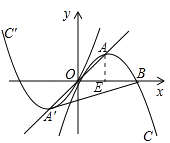
(3)解:作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),
由前可知,抛物线C′的顶点为A′(﹣2,﹣2),
故A′B的中点M的坐标为(1,﹣1).
作MH⊥x轴于H,
∴△MHN∽△BHM,则MH2=HNHB,即12=(1﹣n)(4﹣1),
∴ ![]() ,即N点的坐标为(
,即N点的坐标为( ![]() ,0).
,0).
∵直线l过点M(1,﹣1)、N( ![]() ,0),
,0),
∴直线l的解析式为y=﹣3x+2,
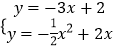 ,解得
,解得 ![]() .
.
∴在抛物线C上存在两点使得PB=PA',其坐标分别为
P1( ![]() ,
, ![]() ),P2(
),P2( ![]() ,
, ![]() );
);
解 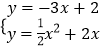 得,
得, ![]() .
.
∴在抛物线C′上也存在两点使得PB=PA',其坐标分别为
P3(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),P4(﹣5﹣
),P4(﹣5﹣ ![]() ,17+3
,17+3 ![]() ).
).
∴点P的坐标是:P1( ![]() ,
, ![]() ),P2(
),P2( ![]() ,
, ![]() ),P3(﹣5+
),P3(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),P4(﹣5﹣
),P4(﹣5﹣ ![]() ,17+3
,17+3 ![]() ).
).

【解析】(1)先连接AB,根据A点是抛物线C的顶点,且C交x轴于O、B,得出AO=AB,再根据∠AOB=60°,得出△ABO是等边三角形,再过A作AE⊥x轴于E,在Rt△OAE中,求出OD、AE的值,即可求出顶点A的坐标,最后设抛物线C的解析式,求出a的值,从而得出抛物线C的解析式;(2)先过A作AE⊥OB于E,根据题意得出OE= ![]() OB=2,再根据直线OA的解析式为y=x,得出AE=OE=2,求出点A的坐标,再将A、B、O的坐标代入y=ax2+bx+c(a<0)中,求出a的值,得出抛物线C的解析式,再根据抛物线C、C′关于原点对称,从而得出抛物线C′的解析式;(3)先作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由(2)知,抛物线C′的顶点为A′(﹣2,﹣2),得出A′B的中点M的坐标,再作MH⊥x轴于H,得出△MHN∽△BHM,则MH2=HNHB,求出N点的坐标,再根据直线l过点M(1,﹣1)、N(
OB=2,再根据直线OA的解析式为y=x,得出AE=OE=2,求出点A的坐标,再将A、B、O的坐标代入y=ax2+bx+c(a<0)中,求出a的值,得出抛物线C的解析式,再根据抛物线C、C′关于原点对称,从而得出抛物线C′的解析式;(3)先作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由(2)知,抛物线C′的顶点为A′(﹣2,﹣2),得出A′B的中点M的坐标,再作MH⊥x轴于H,得出△MHN∽△BHM,则MH2=HNHB,求出N点的坐标,再根据直线l过点M(1,﹣1)、N( ![]() ,0),得出直线l的解析式,求出x的值,再根据抛物线C上存在两点使得PB=PA',从而得出P1 , P2坐标,再根据抛物线C′上也存在两点使得PB=PA',得出P3 , P4的坐标,即可求出答案.
,0),得出直线l的解析式,求出x的值,再根据抛物线C上存在两点使得PB=PA',从而得出P1 , P2坐标,再根据抛物线C′上也存在两点使得PB=PA',得出P3 , P4的坐标,即可求出答案.
【考点精析】本题主要考查了相似三角形的判定与性质和旋转的性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

【题目】某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.

(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
纸盒 纸板 | 竖式纸盒(个) | 横式纸盒(个) |
x | 100﹣x | |
正方形纸板(张) | 2(100﹣x) | |
长方形纸板(张) | 4x |
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.