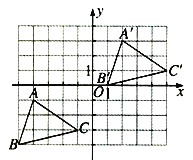
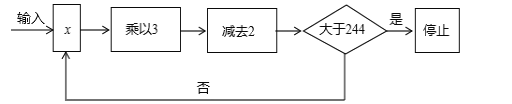
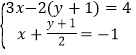题目内容
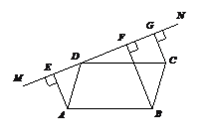
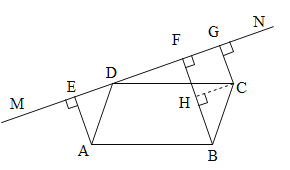
【题目】如图,直线MN过□ABCD的顶点D,过A,B,C三点,分别作MN的垂线,垂足分别是E,F,G.
求证:DE=FG.
【答案】答案见解析
【解析】试题分析:作CH⊥BF与H.可证△AED≌△BHC,得到ED=HC,再由平行线间的距离处处相等得到FG=CH,即可得到结论.
试题解析:证明:作CH⊥BF与H.
∵AE⊥MN,BF⊥MN,∴AE∥BF,∴∠EAD+∠DAB+∠ABF=180°.
∵ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAB+∠ABF+∠HBC=180°,∴∠EAD=∠HBC.在△AED和△BHC中,∵∠EAD=∠HBC,∠AED=∠BHC=90°,AD=BC,∴△AED≌△BHC,∴ED=HC.
∵BF⊥MN,CG⊥MN,∴BF∥CG.
∵GF⊥FB,CH⊥FB,∴FG=CH(平行线间的距离处处相等).
∵ED=HC,∴ED=FG.

练习册系列答案
相关题目