题目内容
（2011•峨眉山市二模）CD是⊙O的直径，AB是一条弦（AB不是直径），已知CD⊥AB，垂足为F，CD=13，AB=12，则CF的长为（ ）
分析：连接OA，求出AF、OA的值，在△AFO中根据勾股定理求出OF，求出CF和DF即可．
解答：解：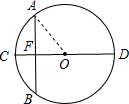
连接OA，
∵CD是直径，CD⊥AB，
∴AF=BF=
AB=6，OA=
CD=6.5，
在Rt△OAF中，由勾股定理得：OF=
=2.5，
∴CF=OC-OF=6.5-2.5=4，
当C在D点时，CF=6.5+2.5=9，
∴CF=4或9，
故选A．
连接OA，
∵CD是直径，CD⊥AB，
∴AF=BF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OAF中，由勾股定理得：OF=
| OA2-AF2 |
∴CF=OC-OF=6.5-2.5=4，
当C在D点时，CF=6.5+2.5=9，
∴CF=4或9，
故选A．
点评：本题考查了垂径定理和勾股定理的应用，关键是求出OF长，注意有两种情况啊，题目比较典型，难度适中．
练习册系列答案
同步练习强化拓展系列答案
相关题目
（2011•峨眉山市二模）如图，直线a，b被直线l所截，已知a∥b，∠1=132°，则∠2等于（ ）
（2011•峨眉山市二模）如图，A、B、C、D都在正方形网格点上，要使△ABC∽△PBD，则点P应在（ ）