Question

如图所示，在四边形ABCD中，∠A=90°，AB=9，BC=20，CD=25，AD=12，求四边形ABCD的面积．

Answer 1

分析：由AB=9，AD=12，∠A=90°可得BD=15．可求得S_△ABC；再由BC=20，CD=25，可得△BCD为直角三角形，进而求得S_△BCD，可求S_{四边形ABCD}=S_△ABD+S_△BCD．

解答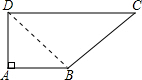：解：如图，连接BD．
∵AB=9，AD=12，∠A=90°，
∴根据勾股定理，得BD=

AD2+AB2

=15．
又∵BC=20，CD=25，
∴CD²=BC²+BD²，
∴∠CBD=90°，
∴S_{四边形ABCD}=S_△ABD+S_△BCD=

1

2

AB•AD+

1

2

BD•BC=

1

2

×9×12+

1

2

×20×15=204．
答：四边形ABCD的面积是204．

点评：本题考查了勾股定理、勾股定理的逆定理．根据已知条件证得△BCD为直角三角形是解题的难点．