��Ŀ����
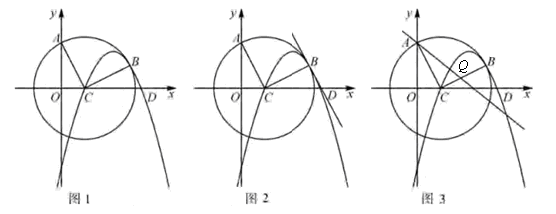
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx��2 ��x�ύ�ڵ�A����1��0����B��4��0������M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN=2����MNΪֱ�DZ�����������ֱ��������CMN����CMN=90�㣮���M�ĺ�����Ϊm��

��1������������������Ӧ�ĺ�����ϵʽ��
��2�����C��������������ʱm��ֵ��
��3�����߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN��
�ٵ���D�����������ߵĶԳ�����ʱ�����D�����꣮
����DNΪֱ�DZ�������ֱ��������DNE������E�����������ߵĶԳ�����ʱ��ֱ��д�����з���������mֵ��
���ο���ʽ��������y=ax2+bx+c��a��0���Ķ�������Ϊ ��
��

��1������������������Ӧ�ĺ�����ϵʽ��
��2�����C��������������ʱm��ֵ��
��3�����߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN��
�ٵ���D�����������ߵĶԳ�����ʱ�����D�����꣮
����DNΪֱ�DZ�������ֱ��������DNE������E�����������ߵĶԳ�����ʱ��ֱ��д�����з���������mֵ��
���ο���ʽ��������y=ax2+bx+c��a��0���Ķ�������Ϊ
 ��
����1��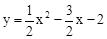 ��
��
��2��m��ֵΪ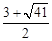 ��
�� ��
��
��3���ٵ�D������Ϊ��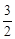 ����2����
����2����
��m��ֵΪm=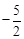 ��m=
��m= ��m=
��m=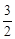 ��m=
��m= ��
��
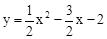 ��
����2��m��ֵΪ
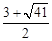 ��
�� ��
����3���ٵ�D������Ϊ��
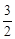 ����2����
����2������m��ֵΪm=
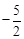 ��m=
��m= ��m=
��m=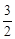 ��m=
��m= ��
�������������1����A����1��0����B��4��0��������������y=ax2+bx��2�����ô���ϵ����������������ߵĽ���ʽ��
��������y=ax2+bx��2������A����1��0����B��4��0����
��
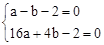 �����
����� ��
��������������Ӧ�ĺ�����ϵʽΪ
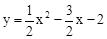 ��
����2�����ݵ���ֱ�������ε����������C������Ϊ��m��2�����ٽ�C���������
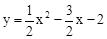 ���������m��ֵ��
���������m��ֵ���ߡ�CMN�ǵ���ֱ�������Σ���CMN=90�㣬��CM=MN=2�����C������Ϊ��m��2����
�ߵ�C��m��2�����������ϣ���
 ��
�����m1=
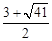 ��m2=
��m2= ��
�����C��������������ʱ��m��ֵΪ
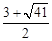 ��
�� ��
����3����������ת�����ʵó���D������Ϊ��m����2�������ݶ��κ������������������
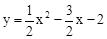 �ĶԳ���Ϊֱ��x=
�ĶԳ���Ϊֱ��x=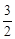 ��Ȼ����ݵ�D��ֱ��x=
��Ȼ����ݵ�D��ֱ��x=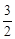 �ϣ����������D�����ꡣ
�ϣ����������D�����ꡣ����ͼ����DNΪֱ�DZ�������ֱ��������DNE��E���λ�������������
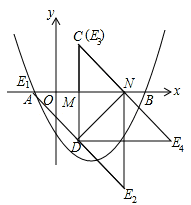
���E����E1��λ��ʱ��
�ߵ�D������Ϊ��m����2����MN=ME1=2����N������Ϊ��m+2��0����
���E1�ģ�m��2��0����
�ߵ�E1��������
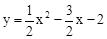 �ĶԳ���x=
�ĶԳ���x=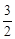 �ϣ�
�ϣ���m��2=
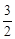 �����m=
�����m= ��
�����E����E2��λ��ʱ��
�ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0����
���E2�ģ�m+2����4����
�ߵ�E2��������
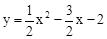 �ĶԳ���x=
�ĶԳ���x=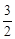 �ϣ���m+2=
�ϣ���m+2=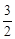 �����m=
�����m= ��
�����E����E3��λ��ʱ��
�ߵ�D������Ϊ��m����2�������E3�ģ�m��2����
�ߵ�E3��������
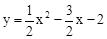 �ĶԳ���x=
�ĶԳ���x=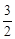 �ϣ���m=
�ϣ���m=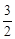 ��
�����E����E4��λ��ʱ��
�ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E4�ģ�m+4����2����
�ߵ�E4��������
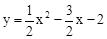 �ĶԳ���x=
�ĶԳ���x=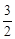 �ϣ���m+4=
�ϣ���m+4=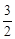 �����m=
�����m=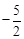 ��
�����Ͽ�֪������E�����������ߵĶԳ�����ʱ�����з���������m��ֵΪm=
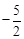 ��m=
��m= ��m=
��m=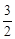 ��m=
��m= ��
��
��ϰ��ϵ�д�
 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д�
�����Ŀ
 �Ķ��������ǡ� ��
�Ķ��������ǡ� ��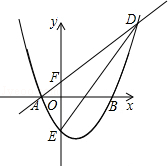
 ������A��
������A�� ��0���͵�B��1��
��0���͵�B��1�� ������x�����һ������ΪC��
������x�����һ������ΪC�� ��MFOʱ����ֱ��д���߶�BM�ij���
��MFOʱ����ֱ��д���߶�BM�ij���
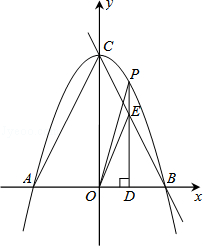
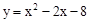 ��y���ڵ�A����x���������ڵ�B��
��y���ڵ�A����x���������ڵ�B��
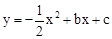 ����C��B���㣬��x�����һ����ΪD��
����C��B���㣬��x�����һ����ΪD��