题目内容
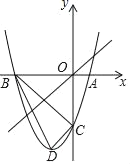
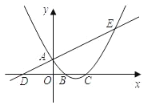
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() );(3)Q点坐标为(1,0)或(
);(3)Q点坐标为(1,0)或(![]() ,0);(4)存在;M点坐标为M(0,﹣8).
,0);(4)存在;M点坐标为M(0,﹣8).
【解析】
(1)求解抛物线的解析式关键是找点,然后将点的坐标带入解析式即可求出解析式;已知B点的坐标,已知A点是直线与抛物线的交点且交于y轴,即可通过直线的解析式求出A点坐标,带入A,B两点坐标即可;(2)最值问题的关键是找对称,通过C点作关于直线AE的对称点F,再连接BF,交AE与点P,此时△PBC周长最小;再求出BF的解析式,再求出与直线AE的交点即可;(3)设出P点的坐标,然后表示出AP、EP的长,求出AE 的长,利用勾股定理得到有关P点的横坐标的方程,求得其横坐标即可;(4)设出M点的坐标,利用C点的距离与到直线AD的距离恰好相等,得到有关M点的纵坐标的方程解得M点的纵坐标即可。
解:(1)∵直线![]() 与y轴交于A,
与y轴交于A,
∴A点的坐标为(0,2),
∵B点坐标为(1,0).
∴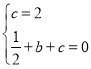 解得:
解得: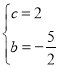
∴![]() ;
;
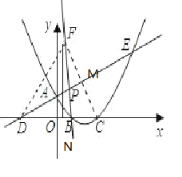
(2)作出C关于直线AE的对称点F,连接BF,CF分别交AE与点P,M,连接DF.过点F做FN垂直于X轴,交X轴于点N.
由题意得点C的坐标为![]() ,点D的坐标为
,点D的坐标为![]()
∵点F是点C关于直线AE的对称点,
∴AE垂直平分CF,
∴直线AE与直线CF的解析式的k值之积为-1,可设直线CF的解析式为![]()
将C点坐标带入可求得CF的解析式为:![]()
将CF和AE的解析式联立可得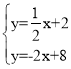 ,解得
,解得![]()
从而求出直线AE与CF的交点M坐标为![]() ,
,
∵M点为CF中点,
所以F点的纵坐标为![]() ,即
,即![]()
∵△CDF为等腰三角形,∴![]()
∴在直角三角形DFN中,由勾股定理得:![]()
∴得![]()
∴N点横坐标为![]()
∴F点的坐标为![]()
∴直线BF的解析式为:![]() ,
,
 ,
,
可得:P(![]() ,
,![]() );
);
(3)根据题意得:![]() ,
,
解得:![]() 或
或![]() ,
,
∴A(0,2),E(6,5),
∴![]() ,
,
设Q(x,0),
①若Q为直角顶点,
则![]() ,
,
即![]() ,
,
此时x无解;
②若点A为直角顶点,
则![]() ,
,
即![]() ,
,
解得:![]() ,
,
即Q(1,0);
③若E为直角顶点,
则![]() ,
,
即![]() ,
,
解得:![]() ,
,
此时求得Q(![]()
![]() ,0);
,0);
∴Q(1,0)或(![]() ,0)
,0)
(4)假设存在,设M坐标为(0,m),则![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴当![]() 时,满足条件,
时,满足条件,
∴在直角三角形AOD中,根据勾股定理得:![]() ,且
,且![]() ,
,![]() ,
,
∵![]() ,
,
∴根据勾股定理得:![]() ,
,
即![]() ,
,
解得![]() ,
,
则M(0,﹣8).

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
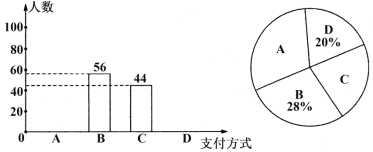
金牌教辅培优优选卷期末冲刺100分系列答案【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?