Question

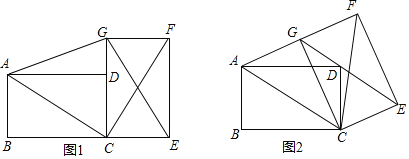
【题目】已知：△ABC内接于⊙O，CD⊥AB于点D．

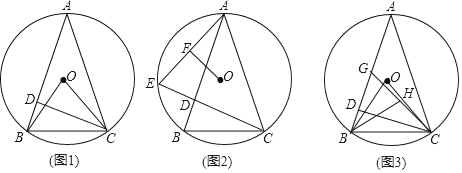
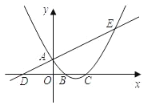
（1）如图1，连接OB和OC，AB＝AC，求证：∠BOC＝4∠BCD；

（2）如图2，延长CD交⊙O于点E，连接AE，过点O作OF⊥AE，垂足为F，求证：BC＝2OF；

（3）如图3，在（1）的条件下，G是AB上一点，连接CG，H为CG的中点，连接BH，若∠BAC＝∠HBA，AG＝8，BH＝9，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）见解析；（3） .

【解析】

（1）如图1中，连接AO，延长AO交BC于H．首先证明∠BCD=∠BAH，再证明∠BOC=4∠BAH即可解决问题．
（2）如图2中，连接AO，延长AO交⊙O于H，连接EH，BH．利用三角形中位线定理证明EH=2OF，再证明BC=EH即可．
（3）如图3中，连接AO，延长AO交BC于K，延长BH交⊙O于T，连接CT，AT，作TQ⊥AB于Q．首先证明CT⊥AB，证明△BHG≌△THC（AAS），推出BH=TH=9，再求出BC，AK即可解决问题．

解：（1）证明：如图1中，连接AO，延长AO交BC于H．

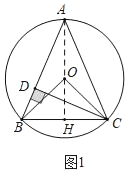
∵AB＝AC，

∴，∠ABC＝∠ACB，

∴AH⊥BC，

∴∠BAH＝∠CAH，

∵CD⊥AB，

∴∠AHB＝∠CDB＝90°，

∴∠CBD+∠ABC＝90°，∠ABC+∠BAH＝90°，

∴∠BCD＝∠BAH，

∵OA＝OB＝OC，

∴∠OAB＝∠OBA＝∠OAC＝∠OCA，

∵∠BOH＝∠OAB+∠OBA，∠COH＝∠OAC+∠OCA，

∴∠BOC＝4∠OAB＝4∠BCD．

（2）证明：如图2中，连接AO，延长AO交⊙O于H，连接EH，BH．

∵OF⊥AE，

∴AF＝FE，

∵AO＝OH，

∴EH＝2OF，

∵AH是直径，

∴∠ABH＝90°，

∵CD⊥AB，

∴∠ADC＝∠ABH＝90°，

∴EC∥BH，

∴∠ECB＝∠CBH，

∴，

∴，

∴EH＝BC，

∴BC＝2OF．

（3）如图3中，连接AO，延长AO交BC于K，延长BH交⊙O于T，连接CT，AT，作TQ⊥AB于Q．

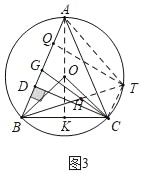
∵∠BTC＝∠BAC，∠BAC＝∠ABH，

∴∠ABH＝∠BTC，

∴AB∥CT，，

∴，BC＝AT，

∴BT＝AC＝AB，

∵∠BHG＝∠THC，∠GBH＝∠CTH，GH＝HC，

∴△BHG≌△THC（AAS），

∴BH＝TH＝9，BG＝CT，

∴AB＝BT＝AC＝18，

∵AG＝8，

∴BG＝CT＝10，

∵TQ⊥AB，CD⊥AB，BC＝AT，易证AQ＝BD＝4，AD＝BQ＝14，

∴BC2＝BD2+CD2＝BD2+AC2﹣AD2＝144，

∴BC＝12，

在Rt△ABK中，AK＝＝＝12，

设OA＝OB＝r，

在Rt△BOK中，则有r2＝62+（12﹣r）2，

∴r＝．