题目内容
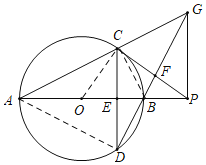
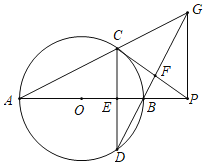
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P是AB延长线上一点,连接PC交DB的延长线于点F,且∠PFB=3∠CAB.
(1)求证:PC是⊙O的切线;
(2)延长AC,DF相交于点G,连接PG,请探究∠CPG和∠CAB的数量关系,并说明理由;
(3)若tan∠CAB=![]() ,CF=5,求⊙O的半径.
,CF=5,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)r=![]()
【解析】
(1)连接OC,由∠PEB=3∠A=∠D+∠DCF,∠D=∠A,得∠DCF=2∠A,∠COB=2∠A,∠DCF=∠COB,因为∠COB+∠OCE=90°,∠DCF+∠OCE=90°,即∠OCP=90°,所以PC是⊙O的切线;
(2)先证明△ACP∽△DCG,所以![]() ,又∠ACD=∠PCG,所以△PCG~△ACD,因此∠CPG=∠CAD=2∠CAB;
,又∠ACD=∠PCG,所以△PCG~△ACD,因此∠CPG=∠CAD=2∠CAB;
(3)由(2)得,PC=PG,∠GPC=∠CAD=∠DCP,所以CD∥PG,于是△GFP~△DFC,又tan∠CAB=![]() ,CF=5,
,CF=5,
设BP=a,PC﹣PG=3a,所以![]() ,CE=
,CE=![]() ,AE=3CE=
,AE=3CE=![]() ,BE=AP﹣BP﹣AE=8a﹣
,BE=AP﹣BP﹣AE=8a﹣![]() ,所以
,所以![]() ,解得
,解得![]() ,所以r=
,所以r=![]() .
.
解:(1)连接OC,
∵∠PEB=3∠A=∠D+∠DCF,
∵∠D=∠A,
∴∠DCF=2∠A,
∴∠COB=2∠A,
∠DCF=∠COB,
∵∠COB+∠OCE=90°,
∴∠DCF+∠OCE=90°,
即∠OCP=90°,
∴PC是⊙O的切线;
(2)∠CPG=2∠CAB.
∵∠BCD=∠CDB=∠CAB=∠ACO,
∠ACP=∠ACO+∠OCP=∠ACO+90°,
∠DCG=∠DCB+∠BCG=∠DCB+90°,
∴∠ACP=∠DCG,
∴△ACP∽△DCG,
∴![]() ,
,
又∵∠ACD=∠PCG,
∴△PCG~△ACD,
∴∠CPG=∠CAD=2∠CAB;
(3)由(2)得,
PC=PG,
∠GPC=∠CAD=∠DCP,
∴CD∥PG,
∴△GFP~△DFC,
∵tan∠CAB=![]() ,CF=5,
,CF=5,
设BP=a,PC﹣PG=3a,
![]() ,
,
![]() ,
,
CE=![]() ,
,
AE=3CE=![]() ,
,
∴BE=AP﹣BP﹣AE=8a﹣![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
AB=8a=![]() ,
,
∴r=![]() .
.