题目内容
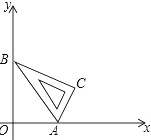
【题目】某渔船向正东方向航行,上午8点在A处时发现渔船、小岛B和小岛C在同一条直线上,渔船以30海里/小时的速度继续向正东方向航行,上午10点到达位于小岛C的正南方向上的D处,此时小岛B在渔船的西偏北63°的方向上,如图,已知小岛C在小岛B的东偏北45°的方向上,求小岛B和小岛C之间的距离.(结果精确到1海里,参考数据:sin63°≈0.9,cos63°≈0.5,tan63°≈2.0,![]() ≈1.4)
≈1.4)
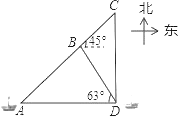
【答案】小岛B和小岛C之间的距离约为84海里.
【解析】
根据题意求得AD=30×2=60海里,过B作BE⊥CD于E,得到CD=AD=60,根据平行线的性质得到∠DBE=∠ADB=63°,根据三角函数的定义得到DE=BEtan63°=2BE,于是得到结论.
由题意得,AD=30×2=60海里,
过B作BE⊥CD于E,
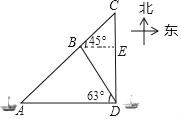
∵∠CBE=45°,
∴∠C=45°,
∵∠AD=90°,
∴∠A=∠C=45°,
∴CD=AD=60,
∵BE⊥CD,AD⊥CD,
∴BE∥AD,
∴∠DBE=∠ADB=63°,
∴DE=BEtan63°=2BE,
∴BE+2BE=CD=60,
∴BE=20,
∴BC=![]() BE=60
BE=60![]() ≈84海里,
≈84海里,
答:小岛B和小岛C之间的距离约为84海里.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目