题目内容
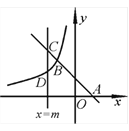
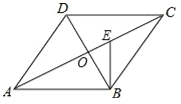
【题目】如图,在矩形ABCD中,AB=3,BE⊥AC于点F,交边AD于点E,连结DF,若点E为AD的中点,则DF的长为__________ .
【答案】3
【解析】分析:过F作FH⊥AD于H.设AE=x,则ED=x.由∠1=∠3,得到tan∠1=![]() =
=![]() =tan∠3=
=tan∠3=![]() =
=![]() ,解方程得到AE的长.由勾股定理得到BE的长.由S△ABE=
,解方程得到AE的长.由勾股定理得到BE的长.由S△ABE=![]() AB×AE=
AB×AE=![]() EB×AF,得到AF的长.再由∠1=∠3,得到sin∠1=sin∠3,从而得到FH、AH、HD的长,即可得到结论.
EB×AF,得到AF的长.再由∠1=∠3,得到sin∠1=sin∠3,从而得到FH、AH、HD的长,即可得到结论.
详解:过F作FH⊥AD于H.设AE=x,则ED=x.
∵∠BAC=90°,∴∠2+∠3=90°.
∵BE⊥AC,∴∠1+∠2=90°,∴∠1=∠3.在Rt△ABE中,tan∠1=![]() =
=![]() .在Rt△ADC中,tan∠3=
.在Rt△ADC中,tan∠3=![]() =
=![]() ,∴
,∴![]() =
=![]() ,解得:x=
,解得:x=![]() (负数舍去).在Rt△ABE中,BE=
(负数舍去).在Rt△ABE中,BE=![]() =
=![]() .
.
∵S△ABE=![]() AB×AE=
AB×AE=![]() EB×AF,∴
EB×AF,∴![]() ,解得:AF=
,解得:AF=![]() .
.
∵∠1=∠3,∴sin∠1=sin∠3,∴![]() ,解得:FH=1,∴AH=
,解得:FH=1,∴AH=![]() =
=![]() =
=![]() ,∴HD=AD-AH=
,∴HD=AD-AH=![]() =
=![]() ,∴FD=
,∴FD=![]() =
=![]() =3.
=3.
故答案为:3.


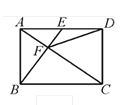
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【题目】一次期中考试中,甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示:(单位:分)
甲 | 乙 | 丙 | 丁 | 戍 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分 的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看, 标准分大的考试成绩更好.请问甲同学在本次考试中,数学与英语哪个学科考 得更好?