��Ŀ����
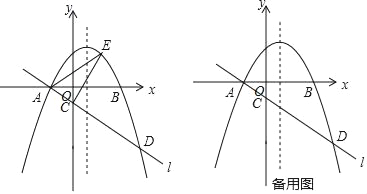
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=kx+h��x���ཻ�ڵ�A����1��0������y���ཻ�ڵ�C����������y=��x2+bx+3��һ����Ϊ��D�������߹�x���ϵ�AB���㣬��CD=4AC��
��1����ֱ��l�������ߵĽ���ʽ��
��2����E��ֱ��l�Ϸ��������ϵ�һ���㣬����ADE������ʱ����E�����ꣻ
��3����P�������߶Գ����ϵ�һ�㣬��Q���������ϣ��ı���APDQ�ܷ�Ϊ���Σ����ܣ���ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��ֱ��l�Ľ���ʽΪy=��x��1����2��E��![]() ��
��![]() ������3��������.
������3��������.
����������������1������ص������������ʽ������⣻
��2������E��EM��x�ᣬ��AD�ڵ�M�����E��m��-m2+2m+3������M��m��-m-1������������ó��������������m�Ķ��κ�������������ֵ���ɣ�
��3���ȸ�������������ı���APDQΪƽ���ı���ʱ��ȷ����P��Q�����꣬�����ù��ɶ������涨�������Ƿ�ֱ���ɣ�
��⣺��1����A��-1��0������y=-x2+bx+3����b=2��
���������ߵĽ���ʽΪy=-x2+2x+3��
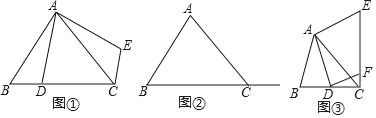
����D��DF��x���ڵ�F����ͼ1
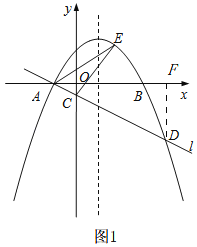
��֤��AOC�ס�AFD��
��![]() ��
��
��CD=4AC��
��![]() ��
��
���D������Ϊ4��
��x=4����y=-x2+2x+3����y=-5��
��D��4��-5����
��x=4��y=-5��x=-1��y=0����y=kx+h��
��ã�k=-1��h=-1��
��ֱ��l�Ľ���ʽΪy=-x-1��
��2������E��EM��x�ᣬ��AD�ڵ�M����ͼ2
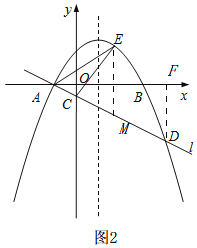
���E��m��-m2+2m+3������M��m��-m-1����
��EM=-m2+2m+3-��-m-1���T-m2+3m+4��
��S��ADE=![]() ��5��-m2+3m+4��=
��5��-m2+3m+4��=![]() m2+
m2+![]() m+10��
m+10��
��m=![]() ʱ����ADE��������
ʱ����ADE��������
��ʱ��E��![]() ��
��![]() ����
����
��3��������
�������£�
�������ߵĶԳ���Ϊֱ��x=1��
��P��1��m����
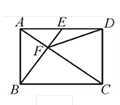
����AD��ƽ���ı���ADPQ��һ���ߣ���ͼ3
����Q��-4��-21����
m=-21-5=-26����P��1��-26����
��ʱAQ2=32+212=450��QP2=52+52=50��AP2=22+262=680��
��AQ2+QP2��AP2��
���AQP��90�㣬
��ʱƽ���ı���ADPQ���Ǿ��Σ�
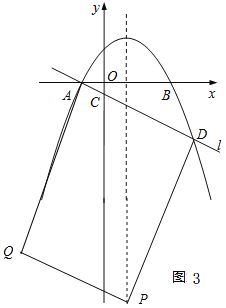
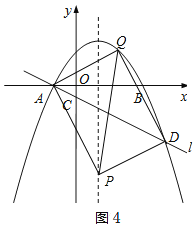
����AD��ƽ���ı���APDQ�ĶԽ��ߣ���ͼ4
����Q��2��3����
m=-5a-3=-8����P��1��-8����
PQ2=12+112=122��PD2=32+32=18QD2=22+82=68��
��PD2+QD2��PQ2��
���PDQ��90�㣬
��ʱƽ���ı���ADPQ���Ǿ��Σ�
�����������ı���APDQ����Ϊ���Σ�

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�