Question

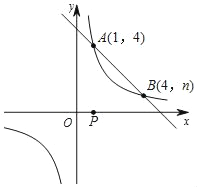
【题目】如图，一次函数y＝kx+b与反比例函数y＝的图象交于A(1，4)，B(4，n)两点．

(1)求反比例函数和一次函数的解析式；

(2)直接写出当x＞0时，kx+b＜的解集．

(3)点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．

Answer 1

【答案】（1）y＝，y=﹣x+5；（2）0＜x＜1或x＞4；（3）点P的坐标为（，0）

【解析】

（1）把A（1，4）代入y=即可求出反比例函数的解析式，再把B（4，n）代入y=得到B（4，1），把A（1，4），B（4，1）代入y=kx+b求得一次函数的解析式；
（2）根据图象以及A、B两点的横坐标即可得出；
（3）作点B关于x轴的对称点B′，连接AB′交x轴于P，则AB′的长度就是PA+PB的最小值，求出直线AB′与x轴的交点即为P点的坐标．

解：（1）把A（1，4）代入y＝，得：m＝4，

∴反比例函数的解析式为y＝；

把B（4，n）代入y＝，得：n＝1，

∴B（4，1），

把A（1，4）、（4，1）代入y＝kx+b，

得：，

解得：，

∴一次函数的解析式为y＝﹣x+5；

（2）根据图象得当0＜x＜1或x＞4，一次函数y＝﹣x+5的图象在反比例函数y＝的下方；

∴当x＞0时，kx+b＜的解集为0＜x＜1或x＞4；

（3）如图，作B关于x轴的对称点B′，连接AB′，交x轴于P，此时PA+PB＝AB′最小，

∵B（4，1），

∴B′（4，﹣1），

设直线AB′的解析式为y＝px+q，

∴，

解得，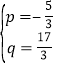

∴直线AB′的解析式为y＝﹣x+，

令y＝0，得﹣x+＝0，

解得x＝，

∴点P的坐标为（，0）．