Question

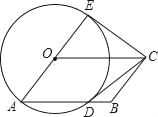
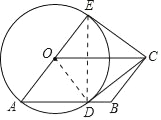
【题目】如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于点D，延长AO交⊙O于点E，连接CD、CE，若CE是⊙O的切线．

（1）求证：CD是⊙O的切线；

（2）若⊙O的半径为4，OC＝7，求BD的长．

Answer 1

【答案】（1）证明见解析；（2）BD=.

【解析】

（1）通过证明△EOC≌△DOC，可得∠ODC=∠OEC=90°，从而得CD是⊙O的切线；（2）连接DE，根据相似三角形的判定和性质解答即可．

（1）证明：连接OD

∵四边形OABC是平行四边形，

∴OC∥AB．

∴∠EOC＝∠A，∠COD＝∠ODA，

∵AO＝DO，

∴∠A＝∠ODA．

∴∠EOC＝∠COD

∵OD＝OE，OC＝OC，

∴△ODC≌△OEC．

∴∠OEC＝∠ODC，

∵CE是⊙O的切线，

∴∠OEC＝90°，

∴∠ODC＝90°．

∵OD是⊙O的半径，

∴CD是⊙O切线；

（2）连接DE，

∵AE是⊙O直径，

∴∠ADE＝90°，

∵∠ODC＝90°．

∴∠ADE＝∠ODC

∵∠COD＝∠ODA，∠A＝∠ODA

∴∠COD＝∠A，

∴△ADE∽△ODC．

∴．

∵⊙O的半径为4，OC＝7．

∴，

∴BD=．