题目内容
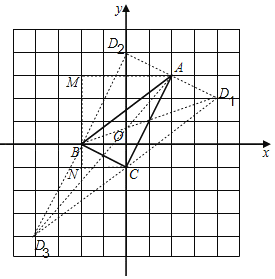
【题目】如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B点坐标为(﹣2,0),C点坐标为(0,﹣1).
(1)S△ABC= ;
(2)若以A、B、C及点D为顶点的四边形为平行四边形,试在图中画出所有D点的位置并求出这些平行四边形中最长的对角线长为 ,最短的对角线长为 .

【答案】(1)5 (2)![]() ;5,画图见详解
;5,画图见详解
【解析】
(1)根据A点坐标为(2,3),B点坐标为(﹣2,0),C点坐标为(0,﹣1),即可求△ABC的面积;
(2)根据平行四边形的判定分三种情况画出图形,求出每个平行四边形的对角线长,即可得结论.
(1)梯形AMNC面积=(2+4)×4÷2=12,
S△NBC=2×1÷2=1,
S△ABM=4×3÷2=6,
S△ABC=梯形AMNC面积﹣S△ABM﹣S△BCN=12﹣1﹣6=5;
(2)点D的位置,如图所示,
由勾股定理得: BD1=![]() =2
=2![]() ,AD3=
,AD3=![]() =
=![]() ,
,
∵CD2=5,
∴平行四边形中最长的对角线长为![]() ,最短的对角线长为5.
,最短的对角线长为5.
故答案为:![]() 、5.
、5.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
【题目】学校为了了解七年级学生的跳绳情况,从七年级学生中随机抽查了![]() 名学生进行
名学生进行![]() 分钟跳绳测试,并对测试结果统计后绘制了如下不完整统计图表.
分钟跳绳测试,并对测试结果统计后绘制了如下不完整统计图表.
组别 | 次数 | 频数(人) | 百分比 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
合计 |
|
| |

请根据图表中的信息解答下列问题:
(1)填空:![]() _________,
_________,![]() __________,
__________,![]() __________;
__________;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生![]() 人,请你估计该校七年级学生跳绳次数在
人,请你估计该校七年级学生跳绳次数在![]() 范围的学生约有多少人?
范围的学生约有多少人?


