��Ŀ����
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=45�㣬AB=4cm����P�ӵ�A��������2cm/s���ٶ��ر�AB���յ�B�˶�������P��PQ��AB������ACB�ڵ�Q��DΪPQ�е㣬��DQΪ�����Ҳ���������DEFQ����������DEFQ���ABC�ص�����ͼ�ε������y��cm2������P���˶�ʱ��Ϊx��s����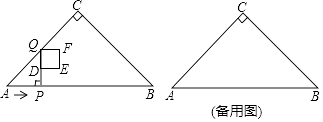
��1������Q�ڱ�AC��ʱ��������DEFQ�ı߳�Ϊcm���ú�x�Ĵ���ʽ��ʾ����
��2������P�����B�غ�ʱ�����F���ڱ�BC��ʱx��ֵ��
��3����0��x��2ʱ����y����x�ĺ�������ʽ��
��4��ֱ��д����BC���е�����������DEFQ�ڲ�ʱx��ȡֵ��Χ��
���𰸡�
��1��x
��2���⣺��ͼ�٣��ӳ�FE��AB��G���������AP=2x��
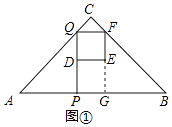
��DΪPQ�е㣬
��DQ=x��
��GP=x��
��2x+x+2x=4��
��x= ![]() ��
��
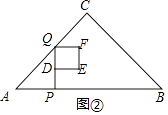
��3���⣺��ͼ�ڣ���0��x�� ![]() ʱ��y=S������DEFQ=DQ2=x2��
ʱ��y=S������DEFQ=DQ2=x2��
��y=x2��
��ͼ�ۣ��� ![]() ��x��1ʱ����C��CH��AB��H����FQ��K����CH=
��x��1ʱ����C��CH��AB��H����FQ��K����CH= ![]() AB=2��
AB=2��
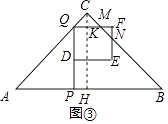
��PQ=AP=2x��CK=2��2x��
��MQ=2CK=4��4x��FM=x����4��4x��=5x��4��
��y=S������DEFQ��S��MNF=DQ2�� ![]() FM2��
FM2��
��y=x2�� ![]() ��5x��4��2=��
��5x��4��2=�� ![]() x2+20x��8��
x2+20x��8��
��y=�� ![]() x2+20x��8��
x2+20x��8��
��ͼ�ܣ���1��x��2ʱ��PQ=4��2x��
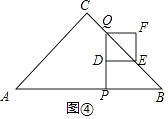
��DQ=2��x��
��y=S��DEQ= ![]() DQ2��
DQ2��
��y= ![]() ��2��x��2��
��2��x��2��
��y= ![]() x2��2x+2��
x2��2x+2��
��4���⣺��Q��C�غ�ʱ��EΪBC���е㣬
��2x=2��
��x=1��
��QΪBC���е�ʱ��BQ= ![]() ��
��
PB=1��
��AP=3��
��2x=3��
��x= ![]() ��
��
���BC���е�����������DEFQ�ڲ�ʱx��ȡֵ��ΧΪ��1��x�� ![]() ��
��
����������1���ߡ�ACB=90�㣬��A=45�㣬PQ��AB��
���AQP=45�㣬
��PQ=AP=2x��
��DΪPQ�е㣬
��DQ=x��
���Դ��ǣ�x��
��2��������⣬����ʾ��ͼ��FG=BG=2x,PQ=AP=2x,��AB=x+2x+2x�������̣����x����3���ɵڣ�2����Ϊ������x=![]() �Ƿֽ�㣬�ֶ�����ʱ�ͷ�Ϊ0��x��
�Ƿֽ�㣬�ֶ�����ʱ�ͷ�Ϊ0��x�� ![]() ��
�� ![]() ��x��1��1��x��2����4���ȼ����е����������ε���������Ϊ���㣬�ֱ��������ʱ��Ӧ��xֵ�����������Χ.
��x��1��1��x��2����4���ȼ����е����������ε���������Ϊ���㣬�ֱ��������ʱ��Ӧ��xֵ�����������Χ.
�����㾫����������Ҫ�����˺�����ϵʽ�ͺ����Ա�����ȡֵ��Χ�����֪ʶ�㣬��Ҫ����������ʾ������ϵ����ѧʽ�ӽ�����������ʽ������ϵʽ��ʹ������������Ա�����ȡֵ��ȫ�壬�����Ա�����ȡֵ��Χ������ȷ�����⣮