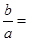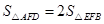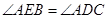题目内容
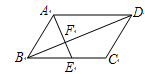
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3,若△A2B1B2、△A3B2B3的面积分别为2和8,则阴影部分的面积和= 。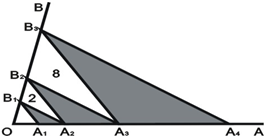

21
试题分析:已知△A2B1B2,△A3B2B3的面积分别为2,8,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底边之比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为8,可求出△A2B2A3的面积,同理可求出△A3B3A4和△A1B1A2的面积.即可求出阴影部分的面积.
∵A2B2∥A3B3,A2B1∥A3B2,
∴∠OB2A2=∠OB3A3,∠A2B1B2=∠A3B2B3,
∴△B1B2A2∽△B2B3A3,
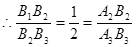
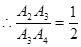
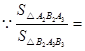
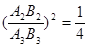 ,,△A3B2B3的面积是8,
,,△A3B2B3的面积是8,∴△A2B2A3的面积为=
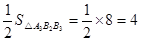
同理可得:△A3B3A4的面积=
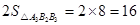
△A1B1A2的面积=
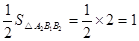
∴三个阴影面积之和=1+4+16=21.
点评:解答本题的关键是利用平行线证明三角形相似,再根据已给的面积,求出相似比,从而求阴影部分的面积.

练习册系列答案
相关题目

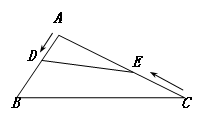

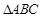 的AB、 AC边上的点,
的AB、 AC边上的点,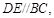 且
且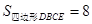
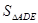 . 那么
. 那么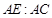 等于 .
等于 .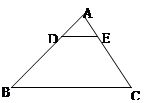
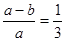 ,则
,则