题目内容
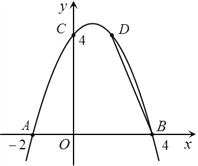
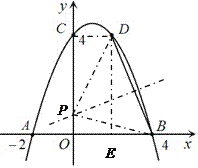
【题目】如图, 已知抛物线![]() 经过A(-2,0)、B(4,0)、C(0,4)三点.
经过A(-2,0)、B(4,0)、C(0,4)三点.
(1)求此抛物线的解析式;
(2)此抛物线有最大值还是最小值?请求出其最大或最小值;
(3)若点D(2,m)在此抛物线上,在y轴的正半轴上是否存在点P,使得△BDP是等腰三角形?若存在,请求出所有符合条件的P点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ;(3)符合条件的
;(3)符合条件的![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】分析:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,运用待定系数法即可求出此抛物线的解析式;
(2)由于二次项系数a=-![]() <0,所以抛物线有最大值,最大值为
<0,所以抛物线有最大值,最大值为![]() ,代入计算即可;
,代入计算即可;
(3)先将点D(2,m)代入(1)中所求的抛物线的解析式,求出m的值,得到点D的坐标,然后假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,再分三种情况进行讨论:①PB=PD;②BP=BD;③DP=DB;每一种情况都可以根据两点间的距离公式列出关于y的方程,解方程即可.
详解:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,得
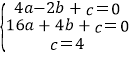 ,
,
解得: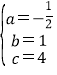 ,
,
所以此抛物线的解析式为y=-![]() x2+x+4;
x2+x+4;
(2)∵y=-![]() x2+x+4,a=-
x2+x+4,a=-![]() <0,
<0,
∴抛物线有最大值,最大值为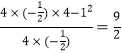 ;
;
(3)∵点D(2,m)在抛物线y=-![]() x2+x+4上,
x2+x+4上,
∴m=-![]() ×22+2+4=4,
×22+2+4=4,
∴D(2,4),
∵B(4,0),
∴BD=![]() .
.
假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,分三种情况:
①如果PB=PD,那么42+y2=22+(y-4)2,解得y=![]() ,
,
所以P1(0,![]() );
);
②如果BP=BD,那么42+y2=20,解得y=±2(负值舍去),
所以P2(0,2);
③如果DP=DB,那么22+(y-4)2=20,解得y=0或8,
y=0不合题意舍去,
y=8时,(0,8)与D,B三点共线,不合题意舍去;
综上可知,所有符合条件的P点的坐标为P1(0,![]() ),P2(0,2).
),P2(0,2).

【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?