题目内容
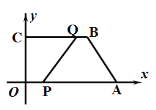
【题目】如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为O（0，0），A（12，0），B（8，6），C（0，6）．动点P从点O出发，以每秒3个单位长度的速度沿边OA向终点A运动；动点Q从点B同时出发，以每秒2个单位长度的速度沿边BC向终点C运动．设运动的时间为t秒，作AG⊥PQ于点G，则AG的最大值为（ ）
A.
B.
C.
D.6
【答案】B
【解析】
连接OB，交PQ于点D，过点D作DF⊥OA于点F，可求出点D的坐标与t无关，由Rt△ADG中
可得AG的最大值为AD，此题得解．
连接OB，交PQ于点D，连接AD，过点D作DF⊥OA于点F，
由题意得
，
∵OC＝6，BC＝8，
∴OB＝
＝10．
∵BQ∥OP，
∴△BDQ∽△ODP，
∴
＝
＝
＝
∴OD＝6．
∵CB∥OA，
∴∠DOF＝∠OBC．
在Rt△OBC中，sin∠OBC＝
＝
＝
，cos∠OBC＝
＝
＝
，
∴OF＝ODcos∠OBC＝6×＝
，DF＝ODsin∠OBC＝6×＝
，
∴点D的坐标为（，），
∴
∴
∵AG⊥PQ
∴
∴当G与D重合时AG的最大，最大值为
，
故选B
练习册系列答案
阅读快车系列答案
相关题目
