题目内容
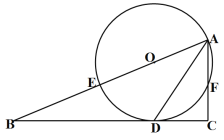
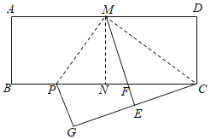
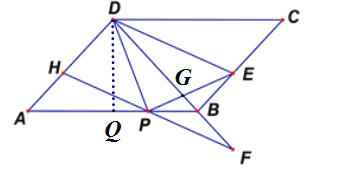
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,过
上一动点,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,将
,将![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
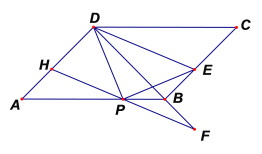
(1)求证:![]() ;
;
(2)当![]() 时,证明
时,证明![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析; (3) ![]()
【解析】
(1)先证B、D、F在一条直线上,再证明∠PDG=∠BEG,接着证∠PDG=∠F得到PD=PF,再证∠ADP =∠DHP得到PD=PH,用等量替换即刻得到答案;
(2)先根据![]() 以及
以及![]() 得到
得到![]() ∽
∽![]() ,再证明
,再证明![]() 以及
以及![]() 得到AD=AP,即可得到
得到AD=AP,即可得到![]() 是等腰三角形;
是等腰三角形;
(3)先根据![]() ,
,![]() ,
,![]() 得到
得到![]() ,再计算DP的长度,利用勾股定理即可得到DE的长.
,再计算DP的长度,利用勾股定理即可得到DE的长.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠PBC=180°,
∵∠A=45°,
∴∠PBC=135°,
由折叠知,∠PBF=∠PBE=135°,
∵![]() ,
,
∴∠ABD=45°,
∴∠ABD+∠PBF=180°,
∴点F在DB的延长线上,
即:B、D、F在一条直线上,
如图,把PE与DF的交点记为G,
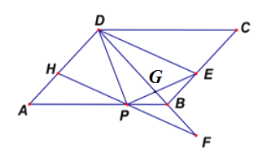
∵∠ABD=45°,∠PBC=135°,
∴∠DBE=90°,
∴∠BEG+∠BGE=90°,∠BGE=∠PGD,
又∵过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,
,
∴∠PDG+∠PGD=90°,
∴∠PDG=∠BEG(等量替换),
又∵∠BEG=∠F,
∴∠PDG=∠F(等量替换),
∴PD=PF,
∵∠GDP+∠ADP=90°,∠F+∠DHP=90°,
∴∠ADP =∠DHP(等量替换),
∴PD=PH,
∴PF=PH;
(2)根据![]() 以及
以及![]() 得到:
得到:
![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
![]()
∴![]() ;
;
(3)∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() (勾股定理),
(勾股定理),
又∵![]() ,
,
∴![]() ,
,![]()
作![]() 于
于![]() ,
,
根据等面积法:![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵△DPE是等腰直角三角形,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
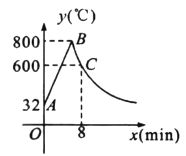
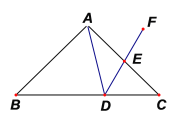
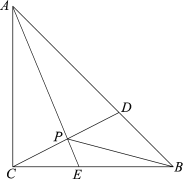
阅读快车系列答案【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
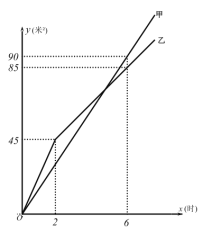
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;
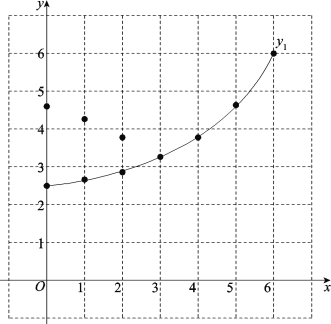
(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
【题目】某社区为了加强社区居民对新型冠状病非肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取![]() 名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:![]()
![]()
乙小区:![]()
![]()
整理数据
成绩 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
统计量 | 平均数 | 中位教 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() _ _;
_ _;
(2)若甲小区共有![]() 人参与答卷,请估计甲小区成绩大于
人参与答卷,请估计甲小区成绩大于![]() 分的人数;
分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由(至少写出一条) .