题目内容
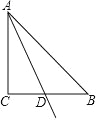
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 D 是 BC 的中点,P 是射线 AD 上的一个动点,则当△BPC 为直角三角形时,AP 的长为____________.
【答案】0或![]() -1或
-1或![]() +1或2
+1或2![]()
【解析】
①当P点与A点重合时,AP=0;②在Rt△ADC中利用勾股定理即可求出AD的长度,再根据直角三角形中斜边上的中线等于斜边的一半即可求出DP的长度,由线段间的关系即可得出AP的长度;当∠CBP=90°时,△PBD≌△ACD,则AD=PD,进一步得到AP的长度.
①当P点与A点重合时,AP=0,
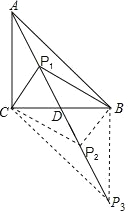
②依照题意画出图形,如图所示.
∵∠ACB=90°,AC=BC=2,D是BC的中点,
∴CD=BD=![]() BC=1,AD=
BC=1,AD=![]() =
=![]() .
.
∵∠BPC=90°,D是BC的中点,
∴DP=![]() BC=1,
BC=1,
∴AP1=ADDP1=![]() 1或AP2=AD+DP2=
1或AP2=AD+DP2=![]() +1.
+1.
当∠CBP3=90°时,△P3BD≌△ACD,
则AD=P3D,
则AP3=2AD=2![]() .
.
故答案为:0或![]() +1或
+1或![]() 1或2
1或2![]() .
.

练习册系列答案
相关题目
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?