��Ŀ����
����Ŀ��������һ�����⣺̽������ ![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С�۸���ѧϰ�����ľ��飬�Ժ��� ![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С�۵�̽�����̣��벹����ɣ�
��1������ ![]() ���Ա���x��ȡֵ��Χ����
���Ա���x��ȡֵ��Χ����
��2���г�y��x�ļ����Ӧֵ����ֱ��д��m��ֵ��m=��
x | �� | -3 | -2 | 0 | 1 | 1��5 | 2��5 | m | 4 | 6 | 7 | �� |
y | �� | 2��4 | 2��5 | 3 | 4 | 6 | -2 | 0 | 1 | 1��5 | 1��6 | �� |
��3������ƽ��ֱ������ϵ ![]() �� ������ϱ��и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��
�� ������ϱ��и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��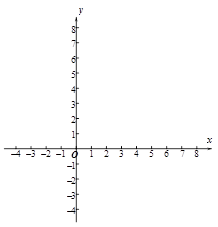
��4����Ϻ�����ͼ��д���ú������������ʣ�
����
�� ��
���𰸡�
��1��![]()
��2��![]()
��3���⣺��ͼ��ʾ��

��4���ú���ͼ������Գ�ͼ��,�ú���ͼ����ԭ��
����������1���� ![]() �ɵó����ۣ���2����2m-6=0�ɵó�m��ֵ����3��������㷨�IJ��軭��������ͼ�ɣ���4���𰸲�Ψһ�����ԴӶԳ��ԡ������ԡ������ԡ���ֵ�������ԡ��������ύ�㡢ͼ���������ȷ�������
�ɵó����ۣ���2����2m-6=0�ɵó�m��ֵ����3��������㷨�IJ��軭��������ͼ�ɣ���4���𰸲�Ψһ�����ԴӶԳ��ԡ������ԡ������ԡ���ֵ�������ԡ��������ύ�㡢ͼ���������ȷ�������
�����������1�� ![]() ��2��
��2�� ![]() ��3����ͼ��ʾ��
��3����ͼ��ʾ��

�� 4 �����ԴӶԳ��ԡ������ԡ������ԡ���ֵ�������ԡ��������ύ�㡢ͼ���������ȷ�������
�����㾫�����������⣬������Ҫ�˽ⷴ����������ͼ��(������������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ��)��