��Ŀ����
����Ŀ����ͼ1����֪��E��F��G��H�ֱ����ı���ABCD����AB��BC��CD��DA���е㣬��������˼·����֤���ı���EFGH��ƽ���ı��Σ�
��1����ͼ2����ͼ1�еĵ�C�ƶ������E�غϵ�λ�ã�F��G��H����BC��CD��DA���е㣬��֤���ı���CFGH��ƽ���ı��Σ�
��2����ͼ3���ڱ߳�Ϊ1��С��������ɵ�5��5�����У���A��C��B���ڸ���ϣ��ڸ���ϻ�����D��ʹ��C��BC��CD��DA���е�F��G��H���������CFGH��
��3���ڣ�2�����������������CFGH�ı߳���
���𰸡�
��1��
֤������ͼ2��
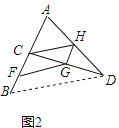
����BD����C��H��AB��DA���е㣬
��CH�ǡ�ABD����λ�ߣ�
��CH��BD��CH= ![]() BD��
BD��
ͬ��FG��BD��FG= ![]() BD��
BD��
��CH��FG��CH=FG��
���ı���CFGH��ƽ���ı���
��2��
��ͼ3��ʾ
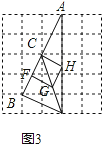
��3��
�⣺��ͼ3����BD= ![]() ����FG=
����FG= ![]() BD=
BD= ![]() ����������CFGH�ı߳���
����������CFGH�ı߳��� ![]()
����������1������BD���������ε���λ�ߵ����ʵõ�CH��BD��CH= ![]() BD��ͬ��FG��BD��FG=
BD��ͬ��FG��BD��FG= ![]() BD����ƽ���ı��ε��ж��������ɵõ����ۣ���2�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ��������3�����ݹ��ɶ����õ�BD=
BD����ƽ���ı��ε��ж��������ɵõ����ۣ���2�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ��������3�����ݹ��ɶ����õ�BD= ![]() ���������ε���λ�ߵ����ʵõ�FG=
���������ε���λ�ߵ����ʵõ�FG= ![]() BD=
BD= ![]() �����ǵõ����ۣ����⿼����ƽ���ı��ε��ж������ʣ������ε����ʣ����ɶ�������ȷ������ͼ���ǽ���Ĺؼ���
�����ǵõ����ۣ����⿼����ƽ���ı��ε��ж������ʣ������ε����ʣ����ɶ�������ȷ������ͼ���ǽ���Ĺؼ���
�����㾫�����������⣬������Ҫ�˽�ƽ���ı��ε��ж�(����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı���)��

 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�����Ŀ������Ժ�칫��2015��3��16�շ����ˡ��й�����ĸ�����巽�����������й�������ʷ�ϵ��ش�ĸΪ�˽�һ���ռ�����֪ʶ�����������Ļ������о����ˡ������У��֪ʶ�������Ϊ�˽�����֪ʶ���ռ�����������ȡ�˲��ֻ���������������õ����в�������ͳ��ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
һ�Ƚ� | 10 | 0.05 |
���Ƚ� | 20 | 0.10 |
���Ƚ� | 30 | b |
��ʤ�� | a | 0.30 |
������ | 80 | 0.40 |
�����������Ϣ������������⣺
��1��a= �� b= �� �Ҳ�ȫƵ���ֲ�ֱ��ͼ��
��2����������ͳ��ͼ�������ֲ�������ʻ����ʤ����Ӧ������Բ�ĽǵĶ����Ƕ��٣�
��3������ξ����У��ס��ҡ���������λͬѧ�����һ�Ƚ�����������λͬѧ�����ѡȡ��λͬѧ�������вμ���һ��������������״ͼ���б��ķ���������ǡ��ѡ�мס��Ҷ��˵ĸ��ʣ�
����Ŀ��ijУ�������Ž�������У�����������������ʽ��A���裬B�赸��C���У�D���֣�ȫУ��ÿ��ѧ����ѡ����һ��������ʽ�����˻��С����ͬѧ��ѡ�õ�������ʽ������������������飬���ݵ���ͳ�ƽ������������ͼ���ֲ�������ͳ��ͼ����
ѡ�� | ��ʽ | �ٷֱ� |
A | ���� | 35% |
B | �赸 | a |
C | ���� | 25% |
D | ���� | 30% |
����ͳ��ͼ�����ش��������⣺
��1�����ε����ѧ�������ˣ�a=�� �� ��������ͳ��ͼ����������
��2�������Уѧ����2000�ˣ�������Ƹ�Уϲ�������衱����������ʽ��ѧ��Լ�ж����ˣ�
��3��ѧУ���õ��鷽ʽ��ÿ����A��B��C��D����������ʽ�У������ȡ���ֽ���չʾ��������״ͼ���б�������ij��鵽��������ʽǡ���ǡ����衱�͡��赸���ĸ��ʣ�




