题目内容
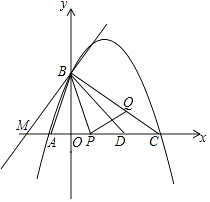
【题目】如图,抛物线经过点A(﹣1,0)和B(0,2 ![]() ),对称轴为x=
),对称轴为x= ![]() .
.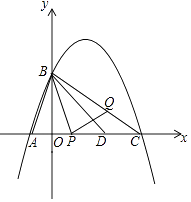
(1)求抛物线的解析式;
(2)抛物线与x轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的度数匀速运动,同时另一动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分?若存在,求出点Q的运动速度;若不存在,请说明理由.
(3)在(2)的前提下,过点B的直线l与x轴的负半轴交于点M,是否存在点M,使以A,B,M为顶点的三角形与△PBC相似?如果存在,请直接写出M的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),
)2+k,(a≠),
把点A(﹣1,0)和B(0,2 ![]() )代入得到
)代入得到 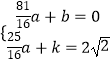 ,
,
解得 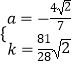 ,
,
∴y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴y=﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]()
(2)
解:令y=0得到﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]() =0,解得x=
=0,解得x= ![]() 或﹣1,
或﹣1,
∴C( ![]() ,0),A(﹣1,0),AB=
,0),A(﹣1,0),AB= ![]() =3,
=3,
∵AD=AB,
∴AD=3,
∴D(2,0),
∵PB被BD垂直平分,
∴BP=BQ,
∴∠DBP=∠DBQ,
∴ ![]() (角平分线的性质定理,可以用面积法证明),
(角平分线的性质定理,可以用面积法证明),
∴ ![]() =
= ![]() ,
,
∴t=2或 ![]() ,
,
∵t<3,
∴t=2,
∴BP=3,BQ=3,
∴VQ= ![]()
(3)
解:存在.理由如下:
由题意P(1,0),PB=3,PC= ![]() ,
,
∵BA=BP=2,
∴∠BAP=∠BPA,
∴∠BPC=∠BAM,
①当 ![]() ,△MAB∽△BPC,
,△MAB∽△BPC,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=OA+AM=
,OM=OA+AM= ![]()
∴M(﹣ ![]() ,0).
,0).
②当 ![]() 时,△MAB∽CPB,
时,△MAB∽CPB,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=AM+OA=
,OM=AM+OA= ![]() ,
,
∴M(﹣ ![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),把点A(﹣1,0)和B(0,2
)2+k,(a≠),把点A(﹣1,0)和B(0,2 ![]() )代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得
)代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得 ![]() (角平分线的性质定理,可以用面积法证明),即
(角平分线的性质定理,可以用面积法证明),即 ![]() =
= ![]() ,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当
,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当 ![]() ,△MAB∽△BPC,列出方程解方程即可.②当
,△MAB∽△BPC,列出方程解方程即可.②当 ![]() 时,△MAB∽CPB,列出方程解方程即可.
时,△MAB∽CPB,列出方程解方程即可.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

 阅读快车系列答案
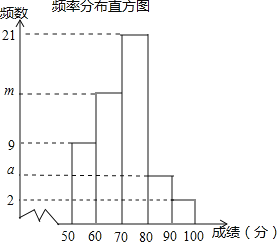
阅读快车系列答案【题目】为参加全区的“我爱古诗词”知识竞赛,王晓所在学校组织了一次古诗词知识测试![]() 王晓从全体学生中随机抽取部分同学的分数
王晓从全体学生中随机抽取部分同学的分数![]() 得分取正整数,满分为100分
得分取正整数,满分为100分![]() 进行统计
进行统计![]() 以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图
以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图![]() 请根据以上频率分布表和布直方图,回答下列问题:
请根据以上频率分布表和布直方图,回答下列问题:
组别 | 分组 | 频数 | 频率 |
1 |
| 9 |
|
2 |
| m | b |
3 |
| 21 |
|
4 |
| a |
|
5 |
| 2 | n |
(1)分别求出a、b、m、n的值;![]() 写出计算过程
写出计算过程![]()
(2)老师说:“王晓的测试成绩是被抽取的同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)得分在![]() 的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?