题目内容
【题目】如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 . 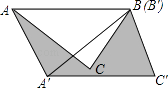
【答案】4 ![]() cm2
cm2
【解析】解:AC与BA′相交于D,如图, 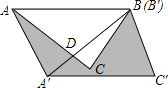
∵△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,
∴∠ABA′=45°,BA′=BA=4,△ABC≌△A′BC′,
∴S△ABC=S△A′BC′ ,
∵S四边形AA′C′B=S△ABC+S阴影部分=S△A′BC′+S△ABA′ ,
∴S阴影部分=S△ABA′ ,
∵∠BAC=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=90°,AD= ![]() AB=2
AB=2 ![]() ,
,
∴S△ABA′= ![]() ADBA′=
ADBA′= ![]() ×2
×2 ![]() ×4=4
×4=4 ![]() (cm2),
(cm2),
∴S阴影部分=4 ![]() cm2 .
cm2 .
故答案为:4 ![]() cm2 .
cm2 .
AC与BA′相交于D,如图,根据旋转的性质得∠ABA′=45°,BA′BA=4,△ABC≌△A′BC′,则S△ABC=S△A′BC′ , 再利用面积的和差可得S阴影部分=S△ABA′ , 接着证明△ADB为等腰直角三角形,得到∠ADB=90°,AD= ![]() AB=2
AB=2 ![]() ,然后利用三角形面积公式计算S△ABA , 从而得到S阴影部分 .
,然后利用三角形面积公式计算S△ABA , 从而得到S阴影部分 .

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目