Question

【题目】如图，△ABC中，AB=AC，BD=CF，BE=CD，∠EDF=a，则下列结论正确的是（　　）

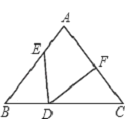
A. a+∠A=90° B. a+∠A=180° C. 2a+∠A=90° D. 2a+∠A=180°

Answer 1

【答案】D

【解析】

根据已知条件可证明△BDE≌△CFD，则∠BED=∠CDF，由∠A+∠B+∠C=180°，得∠B=，因为∠BDE+∠EDF+∠CDF=180°，所以得出a与∠A的关系．

解：在△BDE和△CFD中，，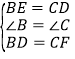

∴△BDE≌△CFD，

∴∠BED=∠CDF，

∵∠A+∠B+∠C=180°，

∴∠B=，

∵∠BDE+∠EDF+∠CDF=180°，

∴180°-∠B-∠BED+a+∠CDF=180°，

∴∠B=a，

即=a，

整理得2a+∠A=180°．

故选：D．