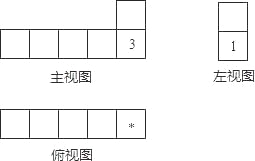
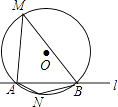��Ŀ����
����Ŀ��������̽����
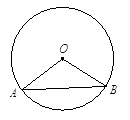
��֪��OΪֱ��AB��һ�㣬������OC����ֱ�����ǰ�ODE������ֱ������(��ͼ��)��ʹֱ�Ƕ������O�غϣ�һ��ֱ�DZ�OD�ص�������OA�ϣ������ǰ��Ƶ�O��ת

��1�������ǰ���ת����ͼ����λ��ʱ����ODƽ����AOC����˵��OEҲƽ����BOC.
��2����OC��AB������Ϊ��O(��ͼ��)����ֱ��д������DOB�����Ľ�
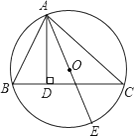
��3������AOC=135��(��ͼ��)�����ǰ��Ƶ�O��˳ʱ������ͼ����λ�ÿ�ʼ��ת����OE��������OB�غϽ���. ��ͨ��������̽��������ת�����У���DOB![]() ��COE�IJ��Ƿ����仯�������䣬����������ֵ�����仯�����ú���n(nΪ���ǰ���ת�Ķ���)�Ĵ���ʽ��ʾ�����.
��COE�IJ��Ƿ����仯�������䣬����������ֵ�����仯�����ú���n(nΪ���ǰ���ת�Ķ���)�Ĵ���ʽ��ʾ�����.
���𰸡���1����ODƽ����AOC�ɵ���AOD=��COD������DOE=90���ɵ���AOD+��EOB=90������COD+��COE=90��������֤�ý�������2����AOD����COE��
��3������n��45������DOB![]() ��COE=135��������n��45������DOB
��COE=135��������n��45������DOB![]() ��COE=225��
��COE=225��![]() 2n
2n
��������
�����������1����ODƽ����AOC�ɵ���AOD=��COD������DOE=90���ɵ���AOD+��EOB=90������COD+��COE=90��������֤�ý��ۣ�
��2����OC��AB�ɵ���AOD+��COD=90��������DOE=90���ɵ���COD+��COE=90�������ɵõ���AOD=��COE���Ӷ������������DOB�����Ľǣ�
��3��������ת45��ʱ��OE��OC�غϣ���Ҫ��n��45����n��45�������������.
��1����ODƽ����AOC
����AOD=��COD
����DOE=90��
����AOD+��EOB=90������COD+��COE=90��
����COE=��EOB
��OEҲƽ����BOC��
��2����OC��AB����DOE=90��
����AOD+��COD=90������COD+��COE=90��
���AOD=��COE
������DOB�����Ľ�Ϊ��AOD����COE��
��3������n��45������DOB![]() ��COE=��180��-n��-��45��-n��=180��-n-45��+n=135����
��COE=��180��-n��-��45��-n��=180��-n-45��+n=135����
����n��45������DOB![]() ��COE=��180��-n��-��n-45����=180��-n-n+45��=225��
��COE=��180��-n��-��n-45����=180��-n-n+45��=225��![]() 2n.
2n.