题目内容
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( ) 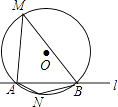
A.2 ![]()
B.4
C.4 ![]()
D.8 ![]()
【答案】C
【解析】解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB= ![]() OA=2
OA=2 ![]() ,
,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB= ![]() ABCD+
ABCD+ ![]() ABCE=
ABCE= ![]() AB(CD+CE)=
AB(CD+CE)= ![]() ABDE=
ABDE= ![]() ×2
×2 ![]() ×4=4
×4=4 ![]() .
.
故选C.
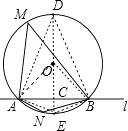
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目