题目内容
【题目】一个七边形棋盘如图所示,7个顶点顺序从0到6编号,称为七个格子.一枚棋子放在0格,现在依逆时针移动这枚棋子,第一次移动1格,第二次移动2格,…,第n次移动n格.则不停留棋子的格子的编号有_____.
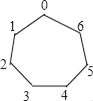
【答案】2,4,5
【解析】
因棋子移动了n次后走过的总格数是1+2+3+…+n=![]() n(n+1),然后再根据题目中所给的第n次依次移动n个顶点的规则,可得到不等式最后求得解.
n(n+1),然后再根据题目中所给的第n次依次移动n个顶点的规则,可得到不等式最后求得解.
解:因棋子移动了n次后走过的总格数是1+2+3+…+n=![]() n(n+1),应停在第
n(n+1),应停在第![]() n(n+1)﹣7p格,
n(n+1)﹣7p格,
这时p是整数,且使0≤![]() n(n+1)﹣7p≤6,分别取n=1,2,3,4,5,6,7时,
n(n+1)﹣7p≤6,分别取n=1,2,3,4,5,6,7时,
![]() n(n+1)﹣7p=1,3,6,3,1,0,0,发现第2,4,5格没有停留棋子,
n(n+1)﹣7p=1,3,6,3,1,0,0,发现第2,4,5格没有停留棋子,
若7<n≤10,设n=7+t(t=1,2,3)代入可得,![]() n(n+1)﹣7p=7m+12t(t+1),
n(n+1)﹣7p=7m+12t(t+1),
由此可知,停棋的情形与n=t时相同,
故第2,4,5格没有停留棋子.
故答案为:2,4,5.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目