Question

【题目】如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=11, 求AD的长.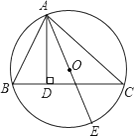

Answer 1

【答案】解：连接CE，则∠E=∠B，

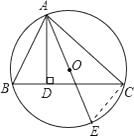
∵AE是⊙O的直径，

∴∠ACE=90°，

又∵AD⊥BC，

∴∠ACE=∠ADB=90°，

∴△ACE∽△ADB，

∴ ，

即 ，

解得AD=

【解析】根据直径所对的圆周角是直角，得到∠ACE=90°，由AD⊥BC，得到△ACE∽△ADB，得到比例，求出AD的值.
【考点精析】根据题目的已知条件，利用圆周角定理和相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．