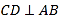题目内容
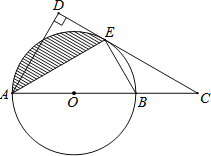
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .
.
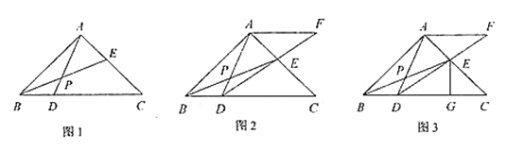
(1)如图1,求证:![]() ;
;
(2)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
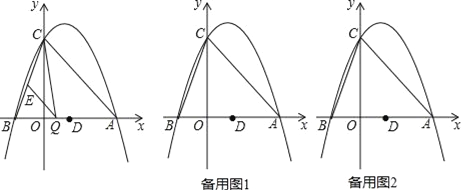
①如图2,求证:![]() ;
;
②如图3,过点![]() 作
作![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长为______.
的长为______.
【答案】(1)证明见解析;(2)①证明见解析;②4.
【解析】
(1)根据三角形的外角性质得到∠APE=∠ABP+∠BAD,得到∠APE=∠ABC,根据等腰三角形的性质得到∠C=∠ABC,等量代换证明结论;
(2)①过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,证明
,证明![]() ,得到EH=EG,根据角平分线的判定定理得到∠ADF=∠CDF,根据平行线的性质、等腰三角形的判定定理证明;
,得到EH=EG,根据角平分线的判定定理得到∠ADF=∠CDF,根据平行线的性质、等腰三角形的判定定理证明;
②根据全等三角形的性质得到PH=GC,DH=DG,结合图形列式计算得到答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
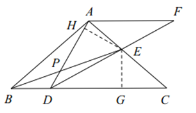
(2))①证明:过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ;
;
②解:如图,作EH⊥AD于H,
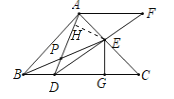
由(2)①可知,△EHP≌△EGC,
∴PH=GC,
在△DEH和△DEG中,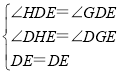 ,
,
∴△DEH≌△DEG(AAS)
∴DH=DG,
∴DG=DH=DP+PH=1+GC,
∴1+GC+GC=7,
解得,GC=3,
∴DG=DC-GC=7-3=4,
故答案为:4.

练习册系列答案
相关题目