��Ŀ����
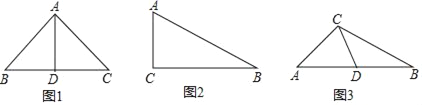
����Ŀ�����壺���������ε�һ��������߶ΰ������ηֳ�����С�����Σ��������һ���������ǵ��������Σ�����һ�������κ�ԭ�����ε������ڽǷֱ���ȣ���ô�������߶ζ���Ϊԭ�����εġ���г�ָ��ߡ���������ͼ1������ֱ��������б���ϵ����߾���һ������г�ָ��ߡ���
��1���жϣ��ԵĴ̡������Ĵ�������
���ȱ������β����ڡ���г�ָ��ߡ��� ��
���������������һ��������һ���ǵ�����������������αش��ڡ���г�ָ��ߡ��� ��
��2����ͼ2��Rt��ABC����C=90�㣬��B=30�㣬AC=2���뻭������г�ָ��ߡ��������㡰��г�ָ��ߡ��ij��ȣ�
��3����ͼ3���߶�CD����ABC�ġ���г�ָ��ߡ�����A=42�㣬����B�Ķ�����
���𰸡���1���̣��̣���2��![]() ����3����B��ֵΪ54���27���46���32�㣮
����3����B��ֵΪ54���27���46���32�㣮
��������
��1����������г�ָ������Ķ��弴���жϣ�
��2����ͼ����CAB��ƽ���ߣ�ֻҪ֤���߶�AD������г�ָ��������ɣ�
��3���������������ۼ��ɣ�
�⣺��1���ٵȱ������β���������г�ָ���������ȷ��
���������������һ��������һ���ǵ�����������������αش�������г�ָ���������ȷ��
�ʴ�Ϊ���̣��̣�
��2����ͼ����CAB��ƽ���ߣ�
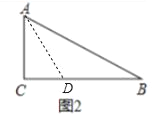
�ߡ�C=90�㣬��B=30�㣬
���DAB=��B=30�㣬
��DA=DB��
���ADB�ǵ��������Σ��ҡ�ACD�ס�BCA��
���߶�AD�ǡ�ABC������г�ָ�������
![]()
��3����ͼ3�У����������Σ�
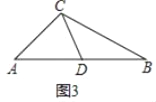
�ٵ�AD=DC����BCD�ס�BACʱ���ɵá�ADC=180�㩁42�㩁42��=96�㣬��BCD=��A=42�㣬
�ߡ�ADC=��BCD+��B��
���B=54�㣮
�ڵ�AC=AD����BCD�ס�BACʱ��ͬ���ɵá�B=27�㣮
�۵�DC=DB����ACD�ס�ABCʱ���ɵá�B=46�㣮
�ܵ�BC=BD����ACD�ס�ABCʱ���ɵá�B=32�㣮
�������������������ġ�B��ֵΪ54����27����46����32�㣮

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�





