Question

【题目】如图，在中，平分交于点，点分别是和上的动点，当，时，的最小值等于__________．

Answer 1

【答案】3

【解析】

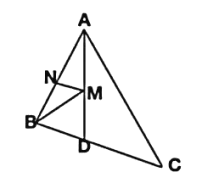
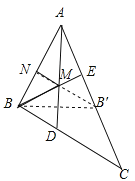
根据AD是∠BAC的平分线确定出点B关于AD的对称点B′在AC上，根据垂线段最短，过点B′作B′N⊥AB于N交AD于M，根据轴对称确定最短路线问题，点M即为使BM+MN最小的点，B′N=BM+MN，过点B作BE⊥AC于E，利用三角形的面积求出BE，再根据等积法可得B′N=BE，从而得解．

解：如图，∵AD是∠BAC的平分线，

∴点B关于AD的对称点B′在AC上，

过点B′作B′N⊥AB于N交AD于M，

由轴对称确定最短路线问题，点M即为使BM+MN最小的点，B′N=BM+MN，

过点B作BE⊥AC于E，

∵AC=8，S△ABC=20，

∴×8BE=12，

解得BE=3，

∵AD是∠BAC的平分线，B′与B关于AD对称，

∴AB=AB′，

∵,

∴B′N=BE=3，

即BM+MN的最小值是3．

故答案为：3．