题目内容
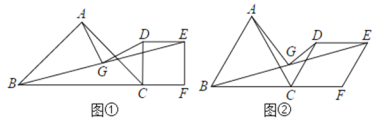
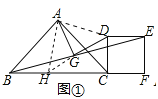
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,AG与DG的位置关系为________,数量关系为________;
(2)如图②,当∠BAC=∠DCF=60°时,AG与DG的位置关系为________,数量关系为________,请证明你的结论.
【答案】(1)AG⊥GD,AG=GD;(2)AG⊥GD,AG=![]() DG.证明见解析.
DG.证明见解析.
【解析】
(1)延长DG与BC交于H,连接AH、AD,通过证得△BGH≌△EGD求得BH=ED,HG=DG,得出BH=DC,然后证得△ABH≌△ACD,得出∠BAH=∠CAD,AH=AD,进而求得∠HAD=90°,即可求得AG⊥GD,AG=GD;
(2)延长DG与BC交于H,连接AH、AD,通过证得△BGH≌△EGD求得BH=ED,HG=DG,得出BH=DC,然后证得△ABH≌△ACD,得出∠BAH=∠CAD,AH=AD,进而求得△HAD是等边三角形,即可证得AG⊥GD,AG=![]() DG.
DG.
(1)AG⊥DG,AG=DG,
证明:延长DG与BC交于H,连接AH、AD,
∵四边形CDEF是正方形,
∴DE=DC,DE∥CF,
∴∠GBH=∠GED,∠GHB=∠GDE,
∵G是BE的中点,
∴BG=EG,
在△BGH和△EGD中
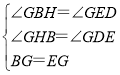
∴△BGH≌△EGD(AAS),
∴BH=ED,HG=DG,
∴BH=DC,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DCF=90°,
∴∠DCB=90°,
∴∠ACD=45°,
∴∠ABH=∠ACD=45°,
在△ABH和△ACD中
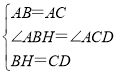
∴△ABH≌△ACD(SAS),
∴∠BAH=∠CAD,AH=AD,
∵∠BAH+∠HAC=90°,
∴∠CAD+∠HAC=90°,即∠HAD=90°,
∴AG⊥GD,AG=GD;
故答案为:AG⊥DG,AG=DG;
(2)AG⊥GD,AG=![]() DG;
DG;
证明:延长DG与BC交于H,连接AH、AD,
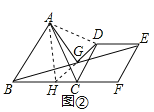
∵四边形CDEF是菱形,
∴DE=DC,DE∥CF,
∴∠GBH=∠GED,∠GHB=∠GDE,
∵G是BE的中点,
∴BG=EG,
在△BGH和△EGD中
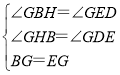
∴△BGH≌△EGD(AAS),
∴BH=ED,HG=DG,
∴BH=DC,
∵AB=AC,∠BAC=∠DCF=60°,
∴∠ABC=60°,∠ACD=60°,
∴∠ABC=∠ACD=60°,
在△ABH和△ACD中
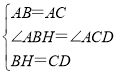
∴△ABH≌△ACD(SAS),
∴∠BAH=∠CAD,AH=AD,
∴∠BAC=∠HAD=60°;
∴AG⊥HD,∠HAG=∠DAG=30°,
∴![]() ,
,
∴![]() .
.
故答案为:AG⊥GD,AG=![]() DG.
DG.

【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元