Question

【题目】已知在长方形ABCD中，AB=4，BC= ，O为BC上一点，BO= ，如图所示，以BC所在直线为x轴，O为坐标原点建立平面直角坐标系，M为线段OC上的一点．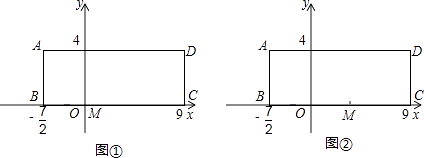

（1）若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P在y轴上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标；
（2）若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P落在长方形ABCD的一边上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标．
（3）若将（2）中的点M的坐标改为（4，0），其它条件不变，如图②，那么符合条件的等腰三角形有几个？求出所有符合条件的点P的坐标．

Answer 1

【答案】
（1）解：∵以OM为一边作等腰△OMP，点P在y轴上，

∴OP=OM，又点M的坐标为（1，0），

∴OP=OM=1，

∴符合条件的等腰三角形有2个，

则点P的坐标为（0，﹣1）、（0，1）；

（2）解：由题意得，OM为等腰△OMP的底边，

则点P在线段OM的垂直平分线上，

∴点P的坐标为：（1，4），

则符合条件的等腰三角形有1个；

（3）解：如图，

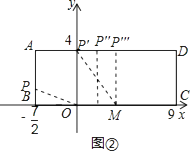
∵OP=OM，

∴OP=4，

∴BP= = ，

∴点P的坐标为（﹣ ， ），

由题意得，P′的坐标为（0，4），P′′的坐标为（1，4），P′′′的坐标为（4，4），

符合条件的等腰三角形有4个．

【解析】（1）抓住已知条件，是以OM为一边作等腰△OMP，且使点P在y轴上，根据等腰直角三角形的性质解答。
（2）根据线段垂直平分线的性质解答即可。
（3）分OM=OP、OP=PM、OM=MP三种情况，根据等腰三角形的性质解答．
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本，需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．