题目内容
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.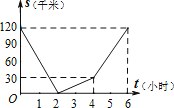
B.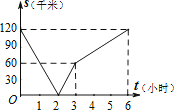
C.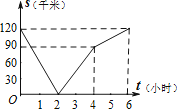
D.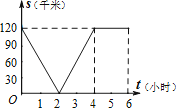
【答案】B
【解析】解:根据题意,两人同时相向出发,甲到达B地时间为:![]() =6小时,乙到达A地:
=6小时,乙到达A地:![]() =3小时.
=3小时.
根据题意,分成两个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地;
相遇前,s=120﹣(20+40)t=120﹣60t(0≤t≤2),当两者相遇时,t=2,s=0,
相遇后,当乙到达A地前,甲乙均在行驶,即s=(20+40)(t﹣2)=60t﹣120(2≤t≤3),当乙到达A地时,此时两者相距60千米;
当乙到达A地后,剩下甲在行驶,即s=60+20(t﹣3)=20t(3≤t≤6),
故: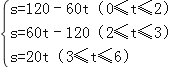
法二:本题可无需列出方程,只需弄清楚题意,分清楚s与t的变化可分为几个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地,故求出各个时间点便可.
∵A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A,
∴两人同时出发,2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,
故两人之间的距离为s(千米),甲行驶的时间为t(小时),则正确反映s与t之间函数关系的是B.
故选:B.
根据题意求出2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,进而根据相遇前、相遇后两个阶段得出相应的分段函数,从而找出符合题意的图象.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】已知 ![]() ,
, ![]() ,
,
(1)当 ![]() 取何值时,
取何值时, ![]() ;
;
(2)当 ![]() 取何值时,
取何值时, ![]() 的值比
的值比 ![]() 的值的3倍大1;
的值的3倍大1;
(3)先填表,后回答:
①
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
②根据所填表格,回答问题:随着 ![]() 的值增大,
的值增大, ![]() 的值逐渐 ,
的值逐渐 , ![]() 的值逐渐 .
的值逐渐 .